题目内容
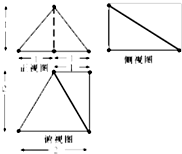
如图是某几何体的三视图,则该几何体的表面积为( )

A、
| ||||||||
B、
| ||||||||
C、4+
| ||||||||
D、
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:由题意,几何体为三棱锥,表面积由4个侧面加一个底面,从而可得几何体的表面积.
解答:
解:由题意,几何体为三棱锥,表面积由4个侧面加一个底面,
∴几何体的表面积为
+3+
+
+
=
+
+
.
故选:A.
∴几何体的表面积为
| 1 |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
| 2 |
3
| ||
| 2 |
故选:A.
点评:本题考查由三视图求几何体的面积、体积,考查对三视图的理解与应用,本题解题的关键是用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,三视图的投影规则是:“主视、俯视 长对正;主视、左视高平齐,左视、俯视 宽相等”,本题是一个基础题.

练习册系列答案
相关题目
已知双曲线
-
=1(a,b>0)的两条渐近线均与圆C:x2+y2-6x+4=0相切,则该双曲线的离心率等于( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知球的直径SC=8,A,B是该球球面上的两点,AB=2
,∠SCA=∠SCB=60°,则三棱锥S-ABC的体积为( )
| 3 |
A、2
| ||
B、4
| ||
C、6
| ||
D、8
|
二项式(2x-
)6的展开式中的常数项是( )
| 1 |
| x |
| A、20 | B、-20 |
| C、160 | D、-160 |
若向量
=(1,-1),
=(2,-1)则|3
-2
|=( )
| a |
| b |
| a |
| b |
A、3
| ||||
B、
| ||||
C、
| ||||
D、3
|
已知集合A={x|-1<x≤2},B={x|y=
-1+ln(2-x)},则A∩B=( )
| x-1 |
| A、(1,2] |
| B、[1,2] |
| C、(1,2) |
| D、[1,2) |
设x、y 满足线性约束条件
,则目标函数z=x-y的最大值为( )
|
| A、-2 | B、-1 | C、0 | D、2 |
定积分
cos2xdx等于( )
| ∫ |
-
|
A、
| ||
B、
| ||
C、
| ||
D、
|