题目内容
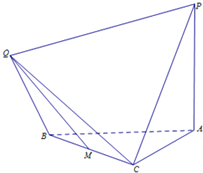 如图,多面体ABCPQ中,PA⊥平面ABC,PA=AB,△ABC是等腰直角三角形,∠BAC=90°,△QBC是等边三角形,M是BC的中点,二面角Q-BC-A的正切值为-
如图,多面体ABCPQ中,PA⊥平面ABC,PA=AB,△ABC是等腰直角三角形,∠BAC=90°,△QBC是等边三角形,M是BC的中点,二面角Q-BC-A的正切值为-| 2 |
(Ⅰ)证明:PQ∥平面ABC;
(Ⅱ)在线段QM上是否存在一点N,使得PN⊥平面QBC,如果存在,请求出N点的位置,如果不存在,请说明理由.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)过点Q做平面ABC的垂线,垂足是H,连结HB,HC,先证明出∠QMH是平面QBC与平面ABC所成的锐二面角,通过已知条件求得PA∥QH且PA=QH,判断出四边形AHQP为矩形,证明出PQ∥AH,最后利用线面平行的判定定理即可.
(Ⅱ)连结PH交QM与N,先证明出BC⊥PN,进而根据三角形相似求得PN⊥QM,利用线面垂直的判定定理证明出PN⊥平面QBC,利用三角形相似的比例关系求得MN=
MQ.
(Ⅱ)连结PH交QM与N,先证明出BC⊥PN,进而根据三角形相似求得PN⊥QM,利用线面垂直的判定定理证明出PN⊥平面QBC,利用三角形相似的比例关系求得MN=
| 1 |
| 3 |
解答:
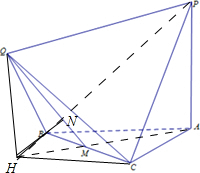
(Ⅰ)证明:过点Q做平面ABC的垂线,
垂足是H,连结HB,HC,
∵QB=QC,
∴HB=HC,
∴HM⊥BC,
又QM⊥BC,
∴∠QMH是平面QBC与平面ABC所成的锐二面角,
且A,M,H共线,tan∠QMH=
,cos∠QMH=
,sin∠QMH=
,
设AC=PA=a,则BC=
a,QM=
•
a,HQ=
•
a•
=a=PA,
又PA∥QH,
∴四边形AHQP为矩形,
∴PQ∥AH,
∵AH?平面ABHC,
∴PQ∥平面ABC.
(Ⅱ)线段QM上存在一点N,使得PN⊥平面QBC,且MN=
MQ,理由如下:
连结PH交QM与N,
BC⊥HM,BC⊥MQ,
∴BC⊥平面QHAP,
∵PN?平面QHAP,
∴BC⊥PN,
矩形PAHQ中,∵M是中点,
∴PA=a,AH=
a,
∴△NMH∽△HPA,
∴∠PHA+∠HMN=90°,
∴PN⊥QM,
又△HNM∽△QHM,
∴MN=
MQ.
垂足是H,连结HB,HC,
∵QB=QC,
∴HB=HC,
∴HM⊥BC,
又QM⊥BC,
∴∠QMH是平面QBC与平面ABC所成的锐二面角,
且A,M,H共线,tan∠QMH=
| 2 |
| 1 |
| 3 |
| ||
|
设AC=PA=a,则BC=
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
| ||
|
又PA∥QH,
∴四边形AHQP为矩形,
∴PQ∥AH,
∵AH?平面ABHC,
∴PQ∥平面ABC.
(Ⅱ)线段QM上存在一点N,使得PN⊥平面QBC,且MN=
| 1 |
| 3 |
连结PH交QM与N,
BC⊥HM,BC⊥MQ,
∴BC⊥平面QHAP,
∵PN?平面QHAP,
∴BC⊥PN,
矩形PAHQ中,∵M是中点,
∴PA=a,AH=
| 2 |
∴△NMH∽△HPA,
∴∠PHA+∠HMN=90°,
∴PN⊥QM,
又△HNM∽△QHM,
∴MN=
| 1 |
| 3 |

点评:本题主要考查了线面平行的判定定理,线面垂直的判定定理.考查了学生基础知识的综合运用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
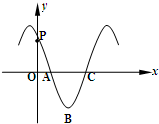 函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中点P为y=f′(x)的图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.
函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中点P为y=f′(x)的图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.