题目内容

现有6名男生和4名女生，根据要求回答下列问题，（结果可用排列组合数或数字回答）
（1）10人站成一排，甲乙两名男生站在一起的排法有多少种？
（2）10人站成一排，任何两名女生都不相邻的排法有多少种？
（3）10人站成一排，男甲不站首位，男乙不站末位的排法有多少种？
（4）现从10人中抽取5人去参加课外社会实践活动，其中至少有3名女生参加的抽法有多少种？
考点：排列、组合及简单计数问题
专题：应用题,排列组合
分析：（1）甲乙两名男生站在一起，利用捆绑法；
（2）任何2名女生都不相邻，利用插空法；
（3）利用直接法或间接法，可得结论；
（4）至少有3名女生参，包括3名或4名两种情况，可得结论．
解答： 解：（1）甲乙两名男生站在一起，利用捆绑法，可得甲乙两名男生站在一起的排法有
A
9
9
A
2
2
；
（2）任何两名女生都不相邻，利用插空法，可得任何两名女生都不相邻的排法有
A
6
6
A
4
7
；
（3）利用直接法或间接法，可得男甲不站首位，男乙不站末位的排法有
A
9
9
+
A
1
8
A
1
8
A
8
8
或
A
10
10
-2
A
9
9
+
A
8
8
；（4）至少有3名女生参，包括3名或4名两种情况，可得至少有3名女生参加的抽法有
C
3
4
C
2
6
+
C
4
4
C
1
6
．
点评：本题考查排列知识的运用，考查捆绑法，插空法，间接法的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
设函数f（x）=2x3-3（a+1）x2+6ax（a∈R）
（1）若f（x）为R上的单调递增函数，求a的值；
（2）若x∈[1，3]时，f（x）的最小值为4，求a的值．
定义在R上的函数f（x）=
1
3
x3+bx2+cx+d（b，c，d∈R）在x=±1处有极值，且其图象过点（0，3）
（Ⅰ）求函数y=f（x）的解析式：
（Ⅱ）设函数g（x）=f′（x）+4lnx-6x+1，若函数y=g（x）的图象与直线y=m有三个不同的交点，求实数m的取值范围．
已知函数f（x）=x2-4x+a+3，g（x）=mx+5-2m，（m∈R，A∈R）
（Ⅰ）求函数y=f（x）在区间[a，a+1]上的最小值；
（Ⅱ）当a=0时，若对任意的x1∈[1，4]，总存在x2∈[1，4]，使f（x1）=g（x2）成立，求实数m的取值范围．
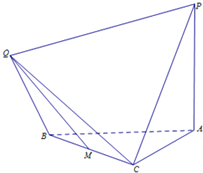如图，多面体ABCPQ中，PA⊥平面ABC，PA=AB，△ABC是等腰直角三角形，∠BAC=90°，△QBC是等边三角形，M是BC的中点，二面角Q-BC-A的正切值为-
2

（Ⅰ）证明：PQ∥平面ABC；
（Ⅱ）在线段QM上是否存在一点N，使得PN⊥平面QBC，如果存在，请求出N点的位置，如果不存在，请说明理由．
甲乙两运动员分别对一目标射击一次，甲射中的概率为0.8，乙射中的概率为0.9，求：
（1）两人都射中的概率；
（2）两人中恰有一人射中的概率；
（3）两人中至少有一人射中的概率；
（4）两人中至多有一人射中的概率．
α、β均为锐角，sinα=
5
13
，cosβ=
4
5
，则sin（α+β）=
 
．
若函数f（x）=|x3-3x-t|（x∈[-2，2]）的最大值为
5
2
，则实数t=
 
．
“a=2”是直线ax+2y+1=0和直线3x+（a+1）y-1=0平行的
 
条件．（在“充分不必要”，“必要不充分”，“充要”，“既不充分又不必要”中选择一个填空）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网