题目内容
已知数列{an}前n项的和Sn=
n2+
n.
(1)求数列{an}的通项公式;
(2)已知n∈N*,证明:2a1+4a2+8a3+…+2nan=(n-1)2n+1+2.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求数列{an}的通项公式;
(2)已知n∈N*,证明:2a1+4a2+8a3+…+2nan=(n-1)2n+1+2.
考点:数学归纳法,等差数列的通项公式,等差数列的前n项和
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:(1)利用公式an=
,由Sn=-2n2+3n,能够求出数列{an}的通项公式.
(2)用数学归纳法证明的步骤证明,验证n=1时等式成立,然后假设n=k(k≥2,k∈N*)时,等式成立,证明n=k+1时等式也成立即可.
|
(2)用数学归纳法证明的步骤证明,验证n=1时等式成立,然后假设n=k(k≥2,k∈N*)时,等式成立,证明n=k+1时等式也成立即可.
解答:
解:(1)∵Sn=
n2+
n,
∴a1=S1=
×12+
×1=1,
an=Sn-Sn-1=(
n2+
n)-[
(n-1)2+
(n-1)]
=n.
当n=1时,a1=1,
∴an=n,
(2)证明:(数学归纳法)
①当n=1时,等式左边=2a1=2,右边=(1-1)21+1+2=2,等式成立.
②假设当n=k(k≥2,k∈N*)等式也成立,即2a1+4a2+8a3+…+2kak=(k-1)2k+1+2
当n=k+1时,2a1+4a2+…+2kak+2k+1ak+1=(k-1)2k+1+2+2k+1(k+1)=2k2k+1+2=(k+1-1)2k+2+2,
这就是说,n=k+1时等式也成立.
由①②可知,对任意的n≥2,n∈N*,原等式均成立.
| 1 |
| 2 |
| 1 |
| 2 |
∴a1=S1=
| 1 |
| 2 |
| 1 |
| 2 |
an=Sn-Sn-1=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=n.
当n=1时,a1=1,
∴an=n,
(2)证明:(数学归纳法)
①当n=1时,等式左边=2a1=2,右边=(1-1)21+1+2=2,等式成立.
②假设当n=k(k≥2,k∈N*)等式也成立,即2a1+4a2+8a3+…+2kak=(k-1)2k+1+2
当n=k+1时,2a1+4a2+…+2kak+2k+1ak+1=(k-1)2k+1+2+2k+1(k+1)=2k2k+1+2=(k+1-1)2k+2+2,
这就是说,n=k+1时等式也成立.
由①②可知,对任意的n≥2,n∈N*,原等式均成立.
点评:本题(1)考查数列的通项公式的求法,是基础题.解题时要认真审题,注意公式an=
,的灵活运用.(2)考查数学归纳法的证明步骤和方法,注意证明n=k+1时,必须用上假设,这是易错点.
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
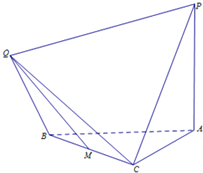 如图,多面体ABCPQ中,PA⊥平面ABC,PA=AB,△ABC是等腰直角三角形,∠BAC=90°,△QBC是等边三角形,M是BC的中点,二面角Q-BC-A的正切值为-
如图,多面体ABCPQ中,PA⊥平面ABC,PA=AB,△ABC是等腰直角三角形,∠BAC=90°,△QBC是等边三角形,M是BC的中点,二面角Q-BC-A的正切值为-