题目内容
1．已知f（2x+1）=4x2+2x+5，则f（-2）=11．分析 由f（-2）=f[2×$（-\frac{3}{2}）$+1]，能求出结果．
解答 解：∵f（2x+1）=4x2+2x+5，
∴f（-2）=f[2×$（-\frac{3}{2}）$+1]=4×$（-\frac{3}{2}）^{2}$+2×$（-\frac{3}{2}）$+5=11．
故答案为：11．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
相关题目
11．若△ABC的内角A、B、C所对的边a、b、c满足（a+b）2-c2=4，且C=60°，则△ABC的面积为（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | 2$\sqrt{3}$-3 | C． | $\frac{\sqrt{3}}{4}$ | D． | $\frac{\sqrt{3}}{6}$ |
9．设集合M={x|x=a}，N={x|ax-1=0}，若M∩N=N，则实数a的值为（ ）
| A． | 1或0 | B． | -1或0 | C． | 1或-1 | D． | 0或1或-1 |
6．设f（x）=3x+3x-8，用二分法求方程3x+3x-8在x∈（1，2）内方程的近似解，则方程的根落在区间（参考数据31.25≈3.95）（ ）
| A． | （1，1.25） | B． | （1.25，1.5） | C． | （1.5，2） | D． | 不能确定 |
10．已知椭圆过点（0，3）且与双曲线$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{7}$=1有相同的焦点，则椭圆的标准方程为（ ）
| A． | $\frac{{x}^{2}}{7}+\frac{{y}^{2}}{9}$=1 | B． | $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{7}$=1 | C． | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{7}$=1 | D． | $\frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}$=1 |
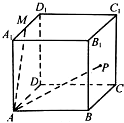在棱长为1的正方体ABCD-A1B1C1D1中，M是A1D1的中点，点P在侧面 BCC1B1上运动．现有下列命题：