题目内容
求下列函数的定义域:
(1)y=log(x-1)(-x2+2x+3);
(2)y=
(a>0,a≠1).
(1)y=log(x-1)(-x2+2x+3);
(2)y=
| 1 | ||
|
考点:对数函数的定义域
专题:分类讨论,函数的性质及应用
分析:(1)根据对数函数的定义,列出不等式组
,求出解集即可;
(2)根据函数y的解析式,结合二次根式与对数函数的性质,列出不等式,求出解集即可.
|
(2)根据函数y的解析式,结合二次根式与对数函数的性质,列出不等式,求出解集即可.
解答:
解:(1)∵y=log(x-1)(-x2+2x+3),
∴
,
解得
,
即1<x<2,或2<x<3,
∴函数y的定义域是(1,2)∪(2,3);
(2)∵y=
(a>0,a≠1),
∴1-loga(x+a)>0,
即loga(x+a)<1;
∴当a>1时,0<x+a<a,解得-a<x<0;
当1>a>0时,x+a>a,解得x>0;
∴a>1时,函数y的定义域是(-a,0),
1>a>0时,函数y的定义域是(0,+∞).
∴
|
解得
|
即1<x<2,或2<x<3,
∴函数y的定义域是(1,2)∪(2,3);
(2)∵y=
| 1 | ||
|
∴1-loga(x+a)>0,
即loga(x+a)<1;
∴当a>1时,0<x+a<a,解得-a<x<0;
当1>a>0时,x+a>a,解得x>0;
∴a>1时,函数y的定义域是(-a,0),
1>a>0时,函数y的定义域是(0,+∞).
点评:本题考查了对数函数的定义、图象与性质的应用问题,也考查了二次根式的被开方数的非负性,分母不为0等基础知识,是综合性题目.

练习册系列答案
相关题目
定积分
(ex+x)dx的值为( )
| ∫ | 2 0 |
| A、e2-1 |
| B、e2 |
| C、e2+1 |
| D、e2+2 |
某化工厂单位要在600名员工中抽取60名员工调查职工身体健康状况,其中青年员工300名,中年员工200名,老年员工100名,下列说法错误的是( )
| A、老年人应作为重点调查对象,故老年人应该抽超过30名 | ||
B、每个人被抽到的概率相同为
| ||
| C、应使用分层抽样抽取样本调查 | ||
| D、抽出的样本能在一定程度上反应总体的健康状况 |
下列不可能是函数图象的是( )
A、 |
B、 |
C、 |
D、 |
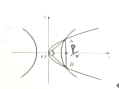 如图,双曲线
如图,双曲线