题目内容
已知函数f(x)=x2+2(a+1)x(x∈[-5,5]),求:
(1)当a=1时,求函数的最大值;
(2)若f(x)在(3,5)上为单调函数,求a的取值范围;
(3)若f(x)>2x,在(3,5)恒成立,求a的取值范围.
(1)当a=1时,求函数的最大值;
(2)若f(x)在(3,5)上为单调函数,求a的取值范围;
(3)若f(x)>2x,在(3,5)恒成立,求a的取值范围.
考点:二次函数的性质,函数恒成立问题
专题:函数的性质及应用
分析:(1)将a=1代入,结合二次函数的图象和性质,分析函数f(x)在[-5,5]上的单调性,进而可得函数的最小值;
(2)若f(x)在(3,5)上为增函数,在区间(3,5)在函数图象对称轴的右侧,由此构造关于a的不等式,解得a的取值范围;
(3)问题转化为a>-
在(3,5)恒成立,从而求出a的范围.
(2)若f(x)在(3,5)上为增函数,在区间(3,5)在函数图象对称轴的右侧,由此构造关于a的不等式,解得a的取值范围;
(3)问题转化为a>-
| x |
| 2 |
解答:
解:(1)当a=1时,f(x)=x2+4x的图象开口朝上,且以直线x=-2为对称轴,
故f(x)在[-5,-2]上为减函数,在[-2,5]上为增函数,
故当x=-2时,函数取最小值-4;
(2)函数f(x)=x2+2(a+1)x的图象开口朝上,且以直线x=-(a+1)为对称轴,
若f(x)在(3,5)上为增函数,
则-(a+1)≤3,
解得:a≥-4;
(3)若f(x)>2x在(3,5)恒成立,
?x2+2ax>0在(3,5)恒成立,
?a>-
在(3,5)恒成立,
?a>-
.
从而a的范围是(-
,+∞).
故f(x)在[-5,-2]上为减函数,在[-2,5]上为增函数,
故当x=-2时,函数取最小值-4;
(2)函数f(x)=x2+2(a+1)x的图象开口朝上,且以直线x=-(a+1)为对称轴,
若f(x)在(3,5)上为增函数,
则-(a+1)≤3,
解得:a≥-4;
(3)若f(x)>2x在(3,5)恒成立,
?x2+2ax>0在(3,5)恒成立,
?a>-
| x |
| 2 |
?a>-
| 3 |
| 2 |
从而a的范围是(-
| 3 |
| 2 |
点评:本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
点P是抛物线y=
x2上的动点,P在直线y=-1上的射影为M,定点A(4,
),则|PA|+|PM|的最小值为( )
| 1 |
| 2 |
| 7 |
| 2 |
A、
| ||
| B、5 | ||
C、
| ||
| D、6 |
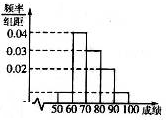 某校200名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100).则成绩在[90,100]内的人数为( )
某校200名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100).则成绩在[90,100]内的人数为( )| A、20 | B、15 | C、10 | D、5 |
已知集合M={x|x-2>0,x∈R},N={y|y=
,x∈R},则M∪N等于( )
| x2+1 |
| A、{x|x≥1} |
| B、{x|1≤x<2} |
| C、{x|x>2} |
| D、{x|x>2或x<0} |