题目内容
15．数y=cosx在[-$\frac{π}{3}$，$\frac{π}{3}$]的值域是（ ）| A． | [-$\frac{1}{2}$，$\frac{1}{2}$] | B． | [-$\frac{1}{2}$，1] | C． | [$\frac{1}{2}$，1] | D． | [-$\frac{1}{2}$，0] |
分析 由条件利用余弦函数的定义域和值域，得出结论．
解答 解：∵x∈[-$\frac{π}{3}$，$\frac{π}{3}$]，可得cosx∈[$\frac{1}{2}$，1]，
故选：C．
点评 本题主要考查余弦函数的定义域和值域，属于基础题．
练习册系列答案
相关题目
6．若奇函数y=g（x）与f（x）=2sin（2x+φ）图象关于直线x=$\frac{π}{6}$对称，要得到y=g（x），则可用y=f（x）的图象变换得到（|φ|＜$\frac{π}{2}$），需经过的变换是（ ）
| A． | 向左平移$\frac{π}{6}$个单位 | B． | 向右平移$\frac{π}{6}$个单位 | ||
| C． | 向左平移$\frac{π}{3}$个单位 | D． | 向右平移$\frac{π}{3}$个单位 |
10．若甲、乙、丙三人中，任选两人参加某项活动，甲被选中的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
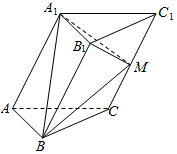在三棱柱ABC-A1B1C1中，侧面A1ACC1⊥底面ABC，M为CC1的中点，∠ABC=90°，AC=A1A，∠A1AC=60°，AB=BC=2．