题目内容

2．已知不等式组$\left\{\begin{array}{l}{x-y≥0}\\{x+y≥0}\\{x≤2}\end{array}\right.$所表示的区域为D，M（x，y）是区域D内的点，点A（-1，2），则z=$\overrightarrow{OA}$•$\overrightarrow{OM}$的最大值为2．

分析 先利用向量数量积公式确定目标函数，然后作出平面区域，根据线性规划的知识可求得z的最大值．

解答 解：z=$\overrightarrow{OA}$•$\overrightarrow{OM}$=-x+2y，
画出满足条件的平面区域，如图示：，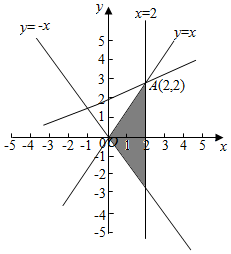


由$\left\{\begin{array}{l}{x=2}\\{x-y=0}\end{array}\right.$，解得A（2，2），
由z=-x+2y得：y=$\frac{1}{2}$x+$\frac{z}{2}$，
显然直线过A（2，2）时，z最大，
z的最大值是2，
故答案为：2．

点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，由平面向量数量积得到线性目标函数是关键，是中档题．

练习册系列答案
相关题目
15．数y=cosx在[-$\frac{π}{3}$，$\frac{π}{3}$]的值域是（　　）
A．[-$\frac{1}{2}$，$\frac{1}{2}$]B．[-$\frac{1}{2}$，1]C．[$\frac{1}{2}$，1]D．[-$\frac{1}{2}$，0]
13．已知F1，F2分别为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左右焦点，过F2作双曲线一条渐近线的垂线，垂足为M，且|MF1|=3|MF2|，则此双曲线的离心率是$\frac{\sqrt{6}}{2}$．
10．已知双曲线的离心率e=$\frac{5}{3}$，点（0，5）为其一个焦点，则该双曲线的标准方程为（　　）
A．$\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{16}$=1B．$\frac{{y}^{2}}{16}$-$\frac{{x}^{2}}{25}$=1C．$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1D．$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1
17．设双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一个顶点为（1，0），它的一个焦点与抛物线y2=8x的焦点相同，则双曲线C的方程为x2-$\frac{{y}^{2}}{3}$=1，离心率为2．
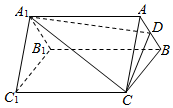7．如图，已知三棱柱ABC-A1BlC1中，点D是AB的中点，平面A1DC分此棱柱成两部分，多面体A1ADC与多面体A1B1C1DBC体积的比值为1：5．
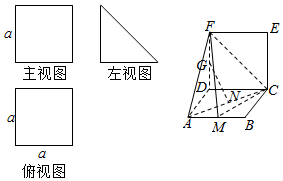14．一个棱柱的直观图和三视图（主视图和俯视图是边长为a的正方形，左视图是直角边长为a的等腰三角形）如图所示，其中M、N分别是AB、AC的中点，G是DF上的一动点．
（1）求证：GN⊥AC；
（2）试确定G点位置使得AG∥平面FMC；
（3）求三棱锥G-MCE的体积．
11．如图，在四棱锥O-ABCD中，底面ABCD是边长为2的正方形，侧棱OB⊥底面ABCD，且侧棱OB的长是2，点E，F，G分别是AB，OD，BC的中点．
（Ⅰ）证明：EF∥平面BOC；
（Ⅱ）证明：OD⊥平面EFG；
（Ⅲ）求三棱锥G-EOF的体积．
12．设全集U=R，已知集合A={-2，-1，0，1，2，3}，B={x|$\frac{3}{x-1}$+1≥0}，则集合A∩∁UB=（　　）
A．{-1，0，1}B．{-1，0}C．{-2，-1，0，1}D．{-1，0，1，2}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网