题目内容
15.已知椭圆$\frac{x^2}{8}+\frac{y^2}{b^2}=1(0<b<2\sqrt{2})$与y轴交于A,B两点,点F为该椭圆的一个焦点,则△ABF面积的最大值为4.分析 由椭圆性质和均值定理得2bc≤b2+c2=8,再由△ABF面积S=bc,能求出△ABF面积的最大值.
解答 解:∵椭圆$\frac{x^2}{8}+\frac{y^2}{b^2}=1(0<b<2\sqrt{2})$与y轴交于A,B两点,点F为该椭圆的一个焦点,
∴b2+c2=8,
∴2bc≤b2+c2=8,bc≤4,
当且仅当b=c时,取等号,
∵△ABF面积S=$\frac{1}{2}×2b×c$=bc≤4.
∴△ABF面积的最大值为4.
故答案为:4.
点评 本题考查三角形面积的最大值的求法,是基础题,解题时要认真审题,注意椭圆性质、均值定理的合理运用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
6.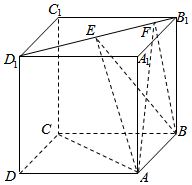 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D1上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D1上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的是( )
 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D1上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F是线段B1D1上的两个动点,且EF=$\frac{\sqrt{2}}{2}$,则下列结论中错误的是( )| A. | AC⊥BF | B. | 三棱锥A-BEF的体积为定值 | ||
| C. | EF∥平面ABCD | D. | 面直线AE、BF所成的角为定值 |
3.设函数$f(x)=\left\{\begin{array}{l}{x^2}-6x+6,x≥0\\ 3x+4,x<0\end{array}\right.$,若互不相等的实数x1,x2,x3满足f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围是( )
| A. | $({\frac{11}{6},6}]$ | B. | $({\frac{11}{3},6})$ | C. | $({\frac{20}{3},\frac{26}{3}})$ | D. | $({\frac{20}{3},\frac{26}{3}}]$ |
20.运行如图所示的程序框图,若输出的点恰有5次落在直线y=x上,则判断框中可填写的条件是( )


| A. | i>6 | B. | i>7 | C. | i>8 | D. | i>9 |
7.设全集为R,集合A={y|y>2},B={x|-1≤x≤4},则(∁RA)∩B=( )
| A. | (2,4] | B. | [-1,2] | C. | [-1,4] | D. | (4,+∞) |
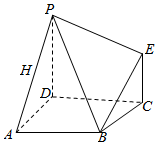 如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$$•\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2.
如图,多面体ABCDPE的底面ABCD是平行四边形,AD=AB=2,$\overrightarrow{AB}$$•\overrightarrow{AD}$=0,PD⊥平面ABCD,EC∥PD,且PD=2EC=2. 已知椭圆C:$\frac{x^2}{4}+{y^2}$=1,点M(x0,y0)是椭圆C上一点,圆M:(x-x0)2+(y-y0)2=r2.
已知椭圆C:$\frac{x^2}{4}+{y^2}$=1,点M(x0,y0)是椭圆C上一点,圆M:(x-x0)2+(y-y0)2=r2.