题目内容
14.要得到函数$y=\sqrt{2}sinx$的图象,只需将函数$y=\sqrt{2}cos(2x-\frac{π}{4})$的图象上所有的点( )| A. | 横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动$\frac{π}{8}$个单位长度 | |
| B. | 横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动$\frac{π}{4}$个单位长度 | |
| C. | 横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),再向右平行移动$\frac{π}{4}$个单位长度 | |
| D. | 横坐标缩短到原来的$\frac{1}{2}$倍(纵坐标不变),再向左平行移动$\frac{π}{8}$个单位长度 |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:要得到函数$y=\sqrt{2}sinx$=$\sqrt{2}$cos(x-$\frac{π}{2}$) 的图象,只需将函数$y=\sqrt{2}cos(2x-\frac{π}{4})$ 的图象上所有的点的横坐标变为原来的2倍,
再再向右平行移动$\frac{π}{4}$个单位长度,即可,
故选:B.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F作倾斜角120°的直线l交椭圆为A,B,若$\overrightarrow{AF}$=2$\overrightarrow{FB}$,则椭圆的离心率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{2}{3}$ |
5.已知x2+y2-4x-2y-4=0,则$\frac{2x+3y+1}{x+2}$的最小值是( )
| A. | -2 | B. | $-\frac{17}{4}$ | C. | $-\frac{29}{5}$ | D. | $2-\frac{{9\sqrt{7}}}{7}$ |
2.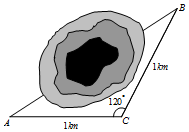 如图,在高速公路建设中需要确定隧道的长度,工程技术人员已测得隧道两端的两点A、B到点C的距离AC=BC=1km,且∠ACB=120°,则A、B两点间的距离为( )
如图,在高速公路建设中需要确定隧道的长度,工程技术人员已测得隧道两端的两点A、B到点C的距离AC=BC=1km,且∠ACB=120°,则A、B两点间的距离为( )
 如图,在高速公路建设中需要确定隧道的长度,工程技术人员已测得隧道两端的两点A、B到点C的距离AC=BC=1km,且∠ACB=120°,则A、B两点间的距离为( )
如图,在高速公路建设中需要确定隧道的长度,工程技术人员已测得隧道两端的两点A、B到点C的距离AC=BC=1km,且∠ACB=120°,则A、B两点间的距离为( )| A. | $\sqrt{3}$km | B. | $\sqrt{2}$km | C. | 1.5km | D. | 2km |
19.函数f(x)=x3-3x2-9x+1的单调递减区间为( )
| A. | (-1,3) | B. | (-∞,-1)或(3,+∞) | C. | (-3,1) | D. | (-∞,-3)或(1,+∞) |
4.x∈R,则x>2的一个必要不充分条件是( )
| A. | x>3 | B. | x<3 | C. | x>1 | D. | x<1 |