题目内容
给定命题p：函数y＝ln[(1－x)(1＋x)]为偶函数；命题q：函数y＝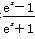
为偶函数，下列说法正确的是( )
A．p∨q是假命题 B．(綈p)∧q是假命题
C．p∧q是真命题 D．(綈p)∨q是真命题
B
[解析] 对于命题p：y＝f(x)＝ln[(1－x)(1＋x)]，令(1－x)(1＋x)＞0，得－1＜x＜1，∴函数f(x)的定义域为(－1,1)，关于原点对称，∵f(－x)＝ln[(1＋x)(1－x)]＝f(x)，
∴函数f(x)为偶函数，∴命题p为真命题；对于命题q：y＝f(x)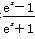＝，函数f(x)的定义域为R，关于原点对称，∵f(－x)＝
＝－f(x)，
∴函数f(x)为奇函数，∴命题q为假命题，∴(綈p)∧q是假命题，故选B.
练习册系列答案
名校课堂系列答案
相关题目
的最小值是( )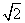
C．4 D．4
＝
，则角C的大小为________．
2”的充要条件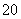
＋x0＋1＜0，则綈p：∀x∈R，x2＋x＋1≥0
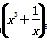5的展开式中含x3的项的系数为60；
－p; 
的球体与棱柱的所有面均相切，那么这个三棱柱的表面积是( )
B．12
的定义域为______________
大型卡车在匀速行驶中每小时耗油量y（升）关于行驶速度x（千米/小时）的函数解析式可以表示为：y=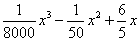
(0<x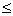
120). 已知甲、乙两地相距100千米。
多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？