题目内容
已知下列命题:
①设m为直线,α,β为平面,且m⊥β,则“m∥α”是“α⊥β”的充要条件;
②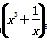 5的展开式中含x3的项的系数为60;
5的展开式中含x3的项的系数为60;
③设随机变量ξ~N(0,1),若P(ξ≥2)=p,则P(-2<ξ<0)= -p;
-p;
④若不等式|x+3|+|x-2|≥2m+1恒成立,则m的取值范围是(-∞,2).
其中真命题的序号是________.(写出所有真命题的序号)
③
[解析] ①因为m⊥β,m∥α⇒α⊥β成立,但由α⊥β,m⊥β,可得到m∥α或m⊂α,故该命题为假命题;②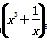 5的展开式中第r+1项Tr+1=C
5的展开式中第r+1项Tr+1=C x15-4r,令15-4r=3,解得r=3,含x3的项的系数为10,故该命题是假命题;③由随机变量ξ~N(0,1),若P(ξ≥2)=p,则P(ξ≤-2)=P(ξ≥2)=p,所以,P(-2<ξ<2)=1-2p,P(-2<ξ<0)=P(0<ξ<2)=
x15-4r,令15-4r=3,解得r=3,含x3的项的系数为10,故该命题是假命题;③由随机变量ξ~N(0,1),若P(ξ≥2)=p,则P(ξ≤-2)=P(ξ≥2)=p,所以,P(-2<ξ<2)=1-2p,P(-2<ξ<0)=P(0<ξ<2)= -p,该命题是真命题;④因|x+3|+|x-2|≥|x+3-(x-2)|=5,故2m+1≤5,解得m≤2,④是假命题.
-p,该命题是真命题;④因|x+3|+|x-2|≥|x+3-(x-2)|=5,故2m+1≤5,解得m≤2,④是假命题.

练习册系列答案
相关题目
 ,求实数k的取值范围.
,求实数k的取值范围.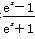 为偶函数,下列说法正确的是( )
为偶函数,下列说法正确的是( )
 B.
B. C.1 D.
C.1 D.

 π B.12π
π B.12π  π
π (
(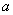 >0,
>0,  , 则
, 则 在
在 上是增函数,则实数
上是增函数,则实数 的取值范围是__________
的取值范围是__________