题目内容
下列函数中，既是奇函数又在定义域内单调递减的函数为（ ）
A、y=
| ||
B、y=
| ||
| C、y=sinx | ||
| D、y=lgx |
考点：函数单调性的判断与证明,函数奇偶性的判断
专题：函数的性质及应用
分析：先求函数的定义域，再通过验证f（-x）和f（x）的关系判断奇偶性；最后可以利用基本初等函数进行单调性的判断．
解答：
解：A、定义域为{x|x≠0}，奇函数，但在定义域上不单调，A错误；
B、定义域为R，f（-x）=-f（x），奇函数，在R上单调递减，B正确；
C、定义域为R，奇函数，但在R上不单调，C错误；
D、定义域为（0，+∞），定义域不关于原点对称，非奇非偶，D错误．
故选：B．
B、定义域为R，f（-x）=-f（x），奇函数，在R上单调递减，B正确；
C、定义域为R，奇函数，但在R上不单调，C错误；
D、定义域为（0，+∞），定义域不关于原点对称，非奇非偶，D错误．
故选：B．
点评：本题考查函数的奇偶性和单调性，都需要考虑定义域，函数奇偶性的前提是要求定义域关于原点对称，单调性则必须在定义域或其子区间上考查．
练习册系列答案
相关题目
已知△ABC中，a，b，c分别是内角A，B，C所对的边，且3a2+3b2-c2=4ab，则下列结论正确的是（ ）
| A、sinA≥cosB |
| B、sinA≥sinB |
| C、sinA≤cosB |
| D、cosA≤cosB |
函数y=
的定义域是（ ）
| 4-log2x |
| A、（0，2] |
| B、（0，16] |
| C、（-∞，2] |
| D、（-∞，16] |
已知函数f（n）=
，则f（5）的值是（ ）
|
| A、4 | B、48 |
| C、240 | D、1440 |
若正数x，y，z满足x2+4y2=z+3xy，则当
取最大值时，
+
-
的最大值为（ ）
| xy |
| z |
| 1 |
| x |
| 1 |
| 2y |
| 1 |
| z |
| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
运行如图所示的程序框图，则输出的所有实数对（x，y）所对应的点都在函数（ ）
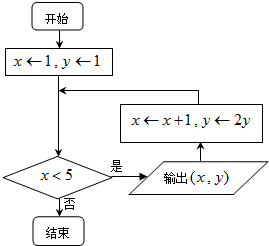
| A、y=x+1的图象上 |
| B、y=2x的图象上 |
| C、y=2x的图象上 |
| D、y=2x-1的图象上 |
不等式x（x-2）≤0的解集是（ ）
| A、[0，2） |
| B、[0，2] |
| C、（-∞，0]∪[2，+∞） |
| D、（-∞，0]∪（2，+∞） |