题目内容
3.若双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1的焦距为10,点P(-2,1)在其渐近线上,则双曲线的方程为( )| A. | $\frac{x^2}{80}$-$\frac{y^2}{20}$=1 | B. | $\frac{x^2}{20}$-$\frac{y^2}{80}$=1 | C. | $\frac{x^2}{20}$-$\frac{y^2}{5}$=1 | D. | $\frac{x^2}{5}$-$\frac{y^2}{20}$=1 |
分析 利用双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1的焦距为10,点P(-2,1)在其渐近线上,建立方程组,求出a,b的值,即可求得双曲线的方程.
解答 解:∵双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1的焦距为10,点P(-2,1)在其渐近线上,
∴a2+b2=25,a=2b,
∴b=$\sqrt{5}$,a=2$\sqrt{5}$
∴双曲线的方程为$\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1.
故选:C.
点评 本题考查双曲线的标准方程,考查双曲线的几何性质,考查学生的计算能力,属于基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
11.若直线a⊥平面α,平面β⊥平面α,则a与β的位置关系为( )
| A. | a与β相交 | B. | a∥β | C. | a?β | D. | a∥β或a?β |
8.曲线y=1+$\sqrt{4-{x}^{2}}$与直线y=k(x+2)+5有两个交点,则实数k的取值范围是( )
| A. | [-1,-$\frac{3}{4}$) | B. | (-∞,-1] | C. | (-$\frac{3}{4}$,0] | D. | [-1,0] |
12.阅读如图的程序框图,运行相应的程序,若输入x的值为2,则输出y的值为( )
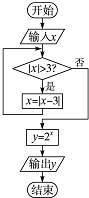

| A. | 0.5 | B. | 1 | C. | 2 | D. | 4 |
13.若函数f(x)=3|x-2|-m-2有唯一的零点,则直线mx+ky+3k-2=0恒过定点为( )
| A. | ($\frac{2}{7},-3$) | B. | (-2,-3) | C. | (0,$\frac{2}{7}$) | D. | (-2,0) |
 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,E为A1A的中点.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD是正方形,E为A1A的中点.