题目内容
8.曲线y=1+$\sqrt{4-{x}^{2}}$与直线y=k(x+2)+5有两个交点,则实数k的取值范围是( )| A. | [-1,-$\frac{3}{4}$) | B. | (-∞,-1] | C. | (-$\frac{3}{4}$,0] | D. | [-1,0] |
分析 根据直线过定点,以及直线和圆的位置关系即可得到结论.
解答 解:由y=k(x+2)+5知直线l过定点(-2,5),将y=1+$\sqrt{4-{x}^{2}}$,移项两边平方得x2+(y-1)2=4(y≥1),
则曲线是以(0,1)为圆心,2为半径,且位于直线y=1上方的半圆.
当直线l过点(2,1)时,直线l与曲线有两个不同的交点
此时k=$\frac{5-1}{-2-2}$=-1,
当直线l与曲线相切时,直线和圆有一个交点,
圆心(0,1)到直线kx-y+5+2k=0的距离d=$\frac{|5+2k|}{\sqrt{{k}^{2}+1}}$=2,
解得k=-$\frac{3}{4}$,
要使曲线y=1+$\sqrt{4-{x}^{2}}$与直线y=k(x+2)+5有两个交点,
则直线l夹在两条直线之间,
因此-1≤k<-$\frac{3}{4}$,
故选:A.
点评 本题主要考查直线和圆的位置关系的应用,考查学生的计算能力,考查点到直线的距离公式的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.若双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1的焦距为10,点P(-2,1)在其渐近线上,则双曲线的方程为( )
| A. | $\frac{x^2}{80}$-$\frac{y^2}{20}$=1 | B. | $\frac{x^2}{20}$-$\frac{y^2}{80}$=1 | C. | $\frac{x^2}{20}$-$\frac{y^2}{5}$=1 | D. | $\frac{x^2}{5}$-$\frac{y^2}{20}$=1 |
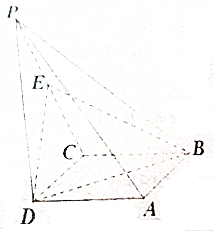 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠DBC=45°,$\frac{BD}{BC}$=$\sqrt{2}$,侧棱PD⊥底面ABCD,PD=CD,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠DBC=45°,$\frac{BD}{BC}$=$\sqrt{2}$,侧棱PD⊥底面ABCD,PD=CD,E是PC的中点.