题目内容
15．
如图，四棱柱ABCD-A1B1C1D1中，底面ABCD是正方形，E为A1A的中点．求证：A1C∥平面EBD．
分析 连结AC，BD，交于点O，连结OE，由三角形中位线定理得OE∥A1C，由此能证明A1C∥平面EBD．
解答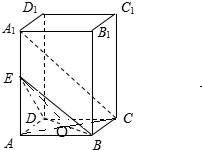 
证明：连结AC，BD，交于点O，连结OE，
∵四棱柱ABCD-A1B1C1D1中，底面ABCD是正方形，
∴O是AC中点，
∵E为A1A的中点，∴OE∥A1C，
∵OE?平面EBD，A1C?平面EBD，
∴A1C∥平面EBD．
点评 本题考查线面平行的证明，是基础题，解题时要认真审题，注意空间思维能力的培养
练习册系列答案
相关题目
3．若双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1的焦距为10，点P（-2，1）在其渐近线上，则双曲线的方程为（ ）
| A． | $\frac{x^2}{80}$-$\frac{y^2}{20}$=1 | B． | $\frac{x^2}{20}$-$\frac{y^2}{80}$=1 | C． | $\frac{x^2}{20}$-$\frac{y^2}{5}$=1 | D． | $\frac{x^2}{5}$-$\frac{y^2}{20}$=1 |
7．在区域$\left\{\begin{array}{l}{0≤x≤1}\\{0≤y≤1}\end{array}\right.$内任意取一点P（x，y），则点P到原点距离小于1的概率是（ ）
| A． | 0 | B． | $\frac{π}{4}$-$\frac{1}{2}$ | C． | $\frac{π}{4}$ | D． | 1-$\frac{π}{4}$ |
4．执行如图所示的程序框图，则输出的A的值为（ ）
| A． | 7 | B． | 31 | C． | 29 | D． | 15 |