题目内容
10.设数列{an}的前n项和为Sn,且an与2Sn的等差中项为1.(1)求数列{an}的通项;
(2)对任意的n∈N*,不等式$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}≥\frac{λ}{{{a_n}^2}}$恒成立,求实数λ的取值范围.
分析 (1)通过等差中项的性质可知an+2Sn=2,进而整理可知数列{an}是首项为$\frac{2}{3}$、公比为$\frac{1}{3}$的等比数列,计算即得结论;
(2)$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{27}{4}$×9n-1,根据等比数列的求和公式,再根据题意可得λ≤$\frac{27}{8}$(1-$\frac{1}{{9}^{n}}$),根据数列的单调性即可求出.
解答 解:(1)∵an是2Sn和1的等差中项,
∴an+2Sn=2,
∴Sn=1-$\frac{1}{2}$an,
当n=1时,a1=1-$\frac{1}{2}$a1,解得a1=$\frac{2}{3}$,
当n≥2时,Sn-1=1-$\frac{1}{2}$an-1,
两式相减得:an=1-$\frac{1}{2}$an-1+$\frac{1}{2}$an-1,
∴an=$\frac{1}{3}$an-1,
∴数列{an}是首项为$\frac{2}{3}$、公比为$\frac{1}{3}$的等比数列,
∴an=2×($\frac{1}{3}$)n;
(2)由(1)可得$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{27}{4}$×9n-1,
∴$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{27}{4}$(1+9+92+…+9n-1)=$\frac{27}{4}$×$\frac{{9}^{n}-1}{8}$,
∵不等式$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}≥\frac{λ}{{{a_n}^2}}$恒成立,
则有$\frac{27}{4}$×$\frac{{9}^{n}-1}{8}$≥$\frac{λ×{9}^{n}}{4}$,即λ≤$\frac{27}{8}$(1-$\frac{1}{{9}^{n}}$),
令f(n)=$\frac{27}{8}$(1-$\frac{1}{{9}^{n}}$),则f(n)在N*上递增,
∴f(n)≥f(1)=3,
∴实数λ的取值范围(-∞,3].
点评 本题考查数列的通项公式和前n项和,以及数列的函数特征,考查了学生的运算能力和转化能力,属于中档题.

| A. | (-∞,-2) | B. | (-∞,-2] | C. | (-∞,4) | D. | (4,+∞) |
| A. | $\frac{3}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |

| A. | 4+4π | B. | 8+4π | C. | $4+\frac{4}{3}π$ | D. | $8+\frac{4}{3}π$ |
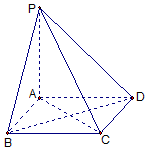 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=AB=2.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=AB=2.