题目内容
设F为抛物线C：y2=3x的焦点，过F且倾斜角为30°的直线交于C于A，B两点，则|AB|=（ ）
A、
| ||||
| B、6 | ||||
| C、12 | ||||
D、7
|
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：求出焦点坐标，利用点斜式求出直线的方程，代入抛物线的方程，利用根与系数的关系，由弦长公式求得|AB|．
解答：
解：由y2=3x得其焦点F（
，0），准线方程为x=-
．
则过抛物线y2=3x的焦点F且倾斜角为30°的直线方程为y=tan30°（x-
）=
（x-
）．
代入抛物线方程，消去y，得16x2-168x+9=0．
设A（x1，y1），B（x2，y2）
则x1+x2=
=
，
所以|AB|=x1+
+x2+
=
+
+
=12
故答案为：12．
| 3 |
| 4 |
| 3 |
| 4 |
则过抛物线y2=3x的焦点F且倾斜角为30°的直线方程为y=tan30°（x-
| 3 |
| 4 |
| ||
| 3 |
| 3 |
| 4 |
代入抛物线方程，消去y，得16x2-168x+9=0．
设A（x1，y1），B（x2，y2）
则x1+x2=
| 168 |
| 16 |
| 21 |
| 2 |
所以|AB|=x1+
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 21 |
| 2 |
故答案为：12．
点评：本题考查抛物线的标准方程，以及简单性质的应用，弦长公式的应用，运用弦长公式是解题的难点和关键．
练习册系列答案
相关题目
已知双曲线C的离心率为2，焦点为F1、F2，点A在C上，若|F1A|=2|F2A|，则cos∠AF2F1=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数中，定义域是R且为增函数的是（ ）
| A、y=e-x |
| B、y=x |
| C、y=lnx |
| D、y=|x| |
阅读如图所示的程序框图，运行相应的程序，输出的n的值为（ ）
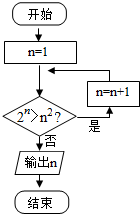
| A、1 | B、2 | C、3 | D、4 |
设x，y满足约束条件
，则z=x+2y的最大值为（ ）
|
| A、8 | B、7 | C、2 | D、1 |
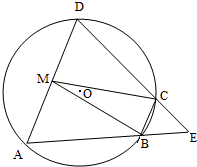如图，四边形ABCD是⊙O的内接四边形，AB的延长线与DC的延长线交于点E，且CB=CE．
如图，某公司要在A、B两地连线上的定点C处建造广告牌CD，其中D为顶端，AC长35米，CB长80米，设点A、B在同一水平面上，从A和B看D的仰角分别为α和β．