题目内容
7．下列函数中，对定义域中的任一实数x均满足f（$\sqrt{2}x$）=2f（x）的是（ ）| A． | f（x）=log2x | B． | f（x）=x|x| | C． | f（x）=x2+1 | D． | f（x）=2x |
分析 将各选项函数解析式，代入f（$\sqrt{2}x$）=2f（x）中验证即可；
解答 解：A：f（$\sqrt{2}x$）=$lo{g}_{2}\sqrt{2}x$=$\frac{1}{2}$+log2x，2f（x）=2log2x，故A不正确；
B：f（$\sqrt{2}x$）=$\sqrt{2}x•|\sqrt{2}x|$=2x|x|，2f（x）=2x|x|，故B正确；
C：f（$\sqrt{2}x$）=2x2+1，2f（x）=2x2+2，故C不正确；
D：f（$\sqrt{2}x$）=${2}^{\sqrt{2}x}$，2f（x）=2•2x=2x+1，故D不正确；
故选：B
点评 本题主要考查了函数基本解析式，以及对数与指数基础运算，属基础题．
练习册系列答案
相关题目
17．①设数列{an}的前n项和为Sn，由an=2n-1，求出S${\;}_{1}={1}^{2}$，S${\;}_{2}={2}^{2}$，S${\;}_{3}={3}^{2}$，…，推断：S${\;}_{n}={n}^{2}$；②由圆x2+y2=r2的面积S=πr2，推断：椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的面积S=πab．则①②两个推理依次是（ ）
| A． | 归纳推理，类比推理 | B． | 演绎推理，类比推理 | ||
| C． | 类比推理，演绎推理 | D． | 归纳推理，演绎推理 |
18．4位同学各自在周五、周六、周日三天中任选一天参加公益活动，则三天都有同学参加公益活动的概率为（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{2}{9}$ | C． | $\frac{4}{9}$ | D． | $\frac{26}{27}$ |
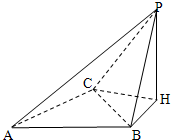如图，在四面体P-ABC，底面ABC是边长为1的正三角形，AB⊥BP，点P在底面ABC上的射影为H，BH=$\frac{\sqrt{3}}{3}$，平面ACP与平面PBH所成的锐二面角的余弦值为$\frac{\sqrt{6}}{3}$．
12．多面体的三视图如图所示，则该多面体的体积为（ ）
| A． | $\frac{16\sqrt{2}}{3}$cm3 | B． | $\frac{32}{3}$cm3 | C． | 16$\sqrt{2}$cm3 | D． | 32cm3 |