题目内容
3.函数f(x)=$\sqrt{{(\frac{1}{2})}^{x}-2}$的定义域是(-∞,-1].分析 根据使函数f(x)=$\sqrt{{(\frac{1}{2})}^{x}-2}$的解析式有意义的原则,构造不等式,解得函数的定义域.
解答 解:若使函数f(x)=$\sqrt{{(\frac{1}{2})}^{x}-2}$的解析式有意义,
自变量x须满足:${(\frac{1}{2})}^{x}-2≥0$,
解得:x∈(-∞,-1],
故函数f(x)=$\sqrt{{(\frac{1}{2})}^{x}-2}$的定义域为:(-∞,-1],
故答案为:(-∞,-1]
点评 本题考查的知识点是函数的定义域,指数不等式的解法,难度中档.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
18.已知向量|$\overrightarrow{AB}$|=2,|$\overrightarrow{CD}$|=1,且|$\overrightarrow{AB}$-2$\overrightarrow{CD}$|=2$\sqrt{3}$,则向量$\overrightarrow{AB}$和$\overrightarrow{CD}$的夹角为( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
15.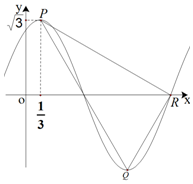 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0),其部分图象如图所示,点P,Q分别为图象上相邻的最高点与最低点,R是图象与x轴的交点,若P点的横坐标为$\frac{1}{3}$,f($\frac{1}{3}$)=$\sqrt{3}$,PR⊥QR,则函数f(x)的解析式可以是( )| A. | $f(x)=\sqrt{3}sin(\frac{π}{2}x+\frac{π}{3})$ | B. | $f(x)=\sqrt{3}sin(\frac{π}{2}x-\frac{π}{6})$ | ||
| C. | $f(x)=\sqrt{3}sin(\frac{2π}{3}x+\frac{5π}{18})$ | D. | $f(x)=\sqrt{3}sin(πx+\frac{π}{6})$ |
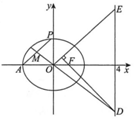 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为为$\frac{1}{2}$,F为椭圆C的右焦点A(-a,0),|AF|=3.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为为$\frac{1}{2}$,F为椭圆C的右焦点A(-a,0),|AF|=3.