题目内容
10.已知函数f(x)=2x2+mx+4,它在(-∞,-2]上单调递减,则f(1)的取值范围是( )| A. | f(1)=14 | B. | f(1)>14 | C. | f(1)≤14 | D. | f(1)≥14 |
分析 由已知得到对称轴x=-$\frac{m}{4}$≥-2,解出m范围,得到f(1)的范围.
解答 解:由已知函数f(x)=2x2+mx+4,m∈R,它在(-∞,-2]上单调递减,
则对称轴x=-$\frac{m}{4}$≥-2,所以m≤8,
又f(1)=6+m,
所以f(1)-6≤8,
所以f(1)≤14,
故选C.
点评 本题考查的知识点是二次函数的性质,其中根据二次函数的图象和性质,构造一个关于m的不等式,是解答本题的关键.

练习册系列答案
相关题目
1.某风险投资公司选择了三个投资项目,设每个项目成功的概率都为$\frac{1}{2}$,且相互之间设有影响,若每个项目成功都获利20万元,若每个项目失败都亏损5万元,该公司三个投资项目获利的期望为( )
| A. | 30万元 | B. | 22.5万元 | C. | 10万元 | D. | 7.5万元 |
18.已知函数f(x)=$\frac{1}{3}$x${\;}^{3}-\frac{1}{2}m{x}^{2}+4x-3$在区间[1,2]上是增函数,则实数m的取值范围为( )
| A. | 4≤m≤5 | B. | 2≤m≤4 | C. | m≤2 | D. | m≤4 |
2.定义在R上的函数f(x)满足f'(x)-f(x)=x•ex,且$f(0)=\frac{1}{2}$,则$\frac{{x•{e^x}}}{f(x)}$的最大值为( )
| A. | 1 | B. | -$\frac{1}{2}$ | C. | -1 | D. | 0 |
20.已知△ABC中,a,b,c分别为内角A,B,C所对的边长,且a=1,b=$\sqrt{2}$,tanC=1,则△ABC外接圆面积为( )
| A. | $\frac{1}{2}$π | B. | $\frac{1}{3}$π | C. | π | D. | $\sqrt{3}$π |
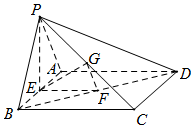 如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD.