题目内容
y=
的值域为 ．
| 1+2sinx |
| sinx-2 |
考点：三角函数的最值
专题：三角函数的求值
分析：利用反表示法可将y=
化为：sinx=
，结合sinx∈[-1，1]得：-1≤
≤1，解分式不等式可得答案．
| 1+2sinx |
| sinx-2 |
| 2y+1 |
| y-2 |
| 2y+1 |
| y-2 |
解答：
解：由y=
得：
ysinx-2y=1+2sinx，
即（y-2）sinx=2y+1，
即sinx=
，
由sinx∈[-1，1]得：-1≤
≤1，
解得：-3≤y≤
，
故y=
的值域为[-3，
]，
故答案为：[-3，
]
| 1+2sinx |
| sinx-2 |
ysinx-2y=1+2sinx，
即（y-2）sinx=2y+1，
即sinx=
| 2y+1 |
| y-2 |
由sinx∈[-1，1]得：-1≤
| 2y+1 |
| y-2 |
解得：-3≤y≤
| 1 |
| 3 |
故y=
| 1+2sinx |
| sinx-2 |
| 1 |
| 3 |
故答案为：[-3，
| 1 |
| 3 |
点评：本题考查的知识点是三角函数的最值和值域，熟练反表示法求函数值域的方法和步骤是解答的关键．
练习册系列答案
金钥匙试卷系列答案
相关题目
已知函数f（x）=x3+ax2-x+c（x∈R），则下列结论错误的是（ ）
| A、函数f（x）一定存在极大值和极小值 | ||||
B、若f（x）在（-∞，x1）、（x2，+∞）上是增函数，则x2-x1≥
| ||||
| C、函数f（x）在点（x0，f（x0））处的切线与f（x）的图象必有两个不同公共点 | ||||
| D、函数f（x）的图象是中心对称图形 |
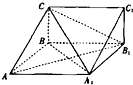如图，在三棱柱ABC-A1B1C1中，四边形A1ABB1为菱形，∠A1AB=45°，四边形BCC1B1为矩形，若AC=5，AB=4，BC=3．
如图，在四棱锥P-ABCD中，底面ABCD是一直角梯形，∠BAD=90°，AB∥DC，PA⊥底面ABCD，且PA=AD=DC=