题目内容
14.已知x,y满足:$\left\{\begin{array}{l}{x≤2}\\{x-2y≥0}\\{x+2y≥0}\end{array}\right.$,则$\frac{2y-x+1}{x+1}$的取值范围是( )| A. | [-1,$\frac{1}{3}$] | B. | [-1,1] | C. | [0,$\frac{1}{3}$] | D. | [0,$\frac{4}{3}$] |
分析 作出不等式组对应的平面区域,$\frac{2y-x+1}{x+1}$=2×$\frac{y+1}{x+1}$-1,设z=$\frac{y+1}{x+1}$,则z的几何意义为动点P(x,y)到点(-1,-1)的斜率,利用数形结合即可得到结论.
解答 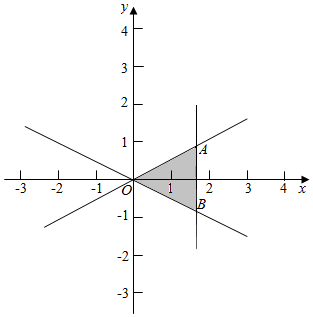 解:作出不等式组对应的平面区域如图.
解:作出不等式组对应的平面区域如图.
$\frac{2y-x+1}{x+1}$=2×$\frac{y+1}{x+1}$-1
设z=$\frac{y+1}{x+1}$,则z的几何意义为动点P(x,y)到点(-1,-1)的斜率,
由图象可知当点P位于点O时,直线的斜率最大为1,
当点P位于点B时,直线的斜率最小为0
即0≤z≤1,
∴-1≤2z-1≤1,
即$\frac{2y-x+1}{x+1}$的取值范围是[-1,1].
故选:B.
点评 本题主要考查线性规划的应用和两点的斜率公式的计算,利用z的几何意义,通过数形结合是解决本题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
5.若θ是第三象限角,且$\sqrt{1+sinθ}$=cos$\frac{θ}{2}$+sin$\frac{θ}{2}$,则$\frac{θ}{2}$是( )
| A. | 第二、四象限 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
2.已知多项式x2+x10=a0+a1(x+1)+a2(x+1)2+…+a9(x+1)9+a10(x+1)10,则a2=( )
| A. | 32 | B. | 42 | C. | 46 | D. | 56 |
9.对于锐角α,若sin(α-$\frac{π}{6}$)=$\frac{1}{3}$,则cos(α-$\frac{π}{3}$)=( )
| A. | $\frac{2\sqrt{6}+1}{6}$ | B. | $\frac{3-\sqrt{2}}{8}$ | C. | $\frac{3+\sqrt{2}}{8}$ | D. | $\frac{2\sqrt{3}-1}{6}$ |
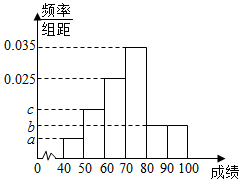 已知某班n名同学的数学测试成绩(单位:分,满分100分)的频率分布直方图如图所示,其中a,b,c成等差数列,且成绩在[90,100]内的有6人.
已知某班n名同学的数学测试成绩(单位:分,满分100分)的频率分布直方图如图所示,其中a,b,c成等差数列,且成绩在[90,100]内的有6人.