题目内容

△ABC的内角A，B，C的对边分别为a，b，c，已知b2+c2-a2+bc=0，则角A等于（　　）
A、
π
3
B、
π
6
C、
2π
3
D、
2π
3
或
π
3
考点：余弦定理
专题：解三角形
分析：根据余弦定理，即可得到结论．
解答： 解：∵b2+c2-a2+bc=0，
∴b2+c2-a2=-bc，
由余弦定理可得cosA=
b2+c2-a2
2bc
=
-bc
2bc
=-
1
2
，
解得A=
2π
3
，
故选：C
点评：本题主要考查余弦定理的应用，比较基础．
练习册系列答案
相关题目
已知幂函数f（x）=x 
3
2
+k-
1
2
k2（k∈z）为偶函数，且在区间（0，+∞）上为增函数，求f（x）的解析式．
已知切线C的极坐标方程是ρ=2，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线L的参数方程为
x=1-
1
2
t
y=2+
3
2
t
（t为参数）．
（1）写出直线L与曲线C的直角坐标系下的方程；
（2）设曲线C经过伸缩变换
x′=x
y′=2y
，得到曲线C′，判断L与切线C′交点的个数．
数列{an}的前n项和为Sn，存在常数A，B，C，使得an+Sn=An2+Bn+C对任意正整数n都成立．
（1）若数列{an}为等差数列，求3A-B+C的值；
（2）若A=-
1
2
，B=-
3
2
，C=1，设bn=an+n数列{nbn}的前n项和为Tn，求Tn；
（3）若C=0，{an}是首项为1的等差数列，设M=
100
i=1
1+
1
ai2
+
1
ai+12
，求不超过M的最大整数的值．
已知二次函数y=x2-4x+a，a是常数，若0≤x＜3，求函数y的取值范围．
若函数f（x）=-|x|在区间[a，+∞﹚上为减函数，则实数a的取值范围是
 
．
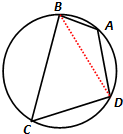已知圆内接四边形ABCD的边AB=1，BC=3，CD=DA=2．
（Ⅰ）求角C的大小和BD的长；
（Ⅱ）求四边形ABCD的面积及外接圆半径．
已知双曲线C：x2-
y2
2
=1，过点A（3，0）作直线l与C交于P、Q两点，若PQ的长等于双曲线C的实轴长的4倍，求l的倾斜角．
tan300°+
cos(-4050)
sin7650
的值是（　　）
A、1+
3
B、1-
3
C、-1-
3
D、-1+
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网