题目内容
定义:如果函数y=f(x)在定义域内给定义域区间[a,b]上存在x0(a<x0<b),满足f(x0)=
,则称函数y=f(x)是[a,b]上的“平均值函数”,0就是它的均值点.给出以下命题:
①函数f(x)=cosx-1是[-2π,2π]上的“平均值函数”
②若y=f(x)是[a,b]上的“平均值函数”,则它的均值点x0≥
.
③若函数f(x)=x-mx-1是[-1,1]上的“平均值函数”,则实数m的取值范围是m∈(0,2)
④若f(x)=lnx是区间[a,b](b>a≥1)上的“平均函数”,x0是它的一个均值点,则lnx0<
.
其中的真命题有 .(写出所有真命题的序号)
| f(b)-f(a) |
| b-a |
①函数f(x)=cosx-1是[-2π,2π]上的“平均值函数”
②若y=f(x)是[a,b]上的“平均值函数”,则它的均值点x0≥
| a+b |
| 2 |
③若函数f(x)=x-mx-1是[-1,1]上的“平均值函数”,则实数m的取值范围是m∈(0,2)
④若f(x)=lnx是区间[a,b](b>a≥1)上的“平均函数”,x0是它的一个均值点,则lnx0<
| 1 | ||
|
其中的真命题有
考点:函数的值
专题:函数的性质及应用
分析:直接利用定义判断①的正误;利用反例判断②的正误;利用定义推出m的范围判断③的正误;利用分析法直接证明结合函数的导数即可证明④的正误.
解答:
解:①函数f(x)=cosx-1是[-2π,2π]上的“平均值函数”,-1就是它的均值点.故①正确;
②不正确.反例:f(x)=x在区间[0,6]上.
③正确.由定义:x02-mx0-1=
,得x02-1=(x0-1)m•m=x0+1,
又x0∈(-1,1)所以实数m的取值范围是m∈(0,2).
④正确.理由如下:由题知lnx0=
.
要证明lnx0<
,
即证明:
<
,
令
=t>1,原式等价于t+lnt2<t-
•2lnt-
.
令h(t)=2lnt-t+
,
则h′(t)=
-1-
,
∴h(t)=2lnt-t+
<h(1)=0,得证.
故答案为:①③④.
②不正确.反例:f(x)=x在区间[0,6]上.
③正确.由定义:x02-mx0-1=
| -m-m |
| 2 |
又x0∈(-1,1)所以实数m的取值范围是m∈(0,2).
④正确.理由如下:由题知lnx0=
| lnb-lna |
| b-a |
要证明lnx0<
| 1 | ||
|
即证明:
| lnb-lna |
| b-a |
| 1 | ||
|
令
|
| 1 |
| t |
| 1 |
| t |
令h(t)=2lnt-t+
| 1 |
| t |
则h′(t)=
| 2 |
| t |
| 1 |
| t2 |
∴h(t)=2lnt-t+
| 1 |
| t |
故答案为:①③④.
点评:本题考查新定义的应用,函数的导数以及分析法的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、命题“若x=y,则sinx≠siny”的逆否命题为假命题 |
| D、命题“若x2+y2≠0,则x、y不全为零”的否命题为真命题 |
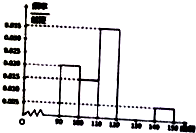 某校高三数学竞赛初赛考试后,对考生的成绩进行统计(考生成绩均不低于90分,满分为150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…,第六组[140,150],如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
某校高三数学竞赛初赛考试后,对考生的成绩进行统计(考生成绩均不低于90分,满分为150分),将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…,第六组[140,150],如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
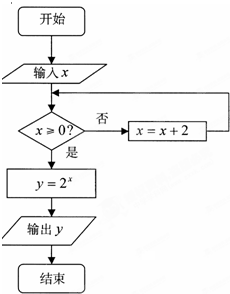 如图所示的算法流程图中(注:“x=x+2”也可写成“x:=x+2”,均表示赋值语句),若输入的x值为-3,则输出的y值是( )
如图所示的算法流程图中(注:“x=x+2”也可写成“x:=x+2”,均表示赋值语句),若输入的x值为-3,则输出的y值是( )