题目内容
已知af（x）+f（-x）=bx，求f（x）的表达式．
考点：函数解析式的求解及常用方法
专题：计算题,函数的性质及应用
分析：观察题目给定的条件，将x换为-x，通过方程的观点解出f（x）的解析式．
解答：
解：∵af（x）+f（-x）=bx①，
∴af（-x）+f（x）=-bx②，
①×a-②化简得，
（a2-1）f（x）=b（a+1）x，
若a2-1=0，不成立；
故a≠±1，
∴f（x）=
x=
x．
∴af（-x）+f（x）=-bx②，
①×a-②化简得，
（a2-1）f（x）=b（a+1）x，
若a2-1=0，不成立；
故a≠±1，
∴f（x）=
| b(a+1) |
| a2-1 |
| b |
| a-1 |
点评：本题考查了函数解析式的求法，通过解方程的方式求解析式是重要的方法，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f（x）=（
）x-x
，那么在下列区间中含有函数f（x）零点的是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
A、（
| ||||
B、（
| ||||
C、（
| ||||
D、（0，
|
在△ABC中，A，B，C的对边分别是a，b，c，其中a=
，b=
，sinB=
，则角A的取值范围一定属于（ ）
| 5 |
| 3 |
| ||
| 2 |
| A、（45°，90°） |
| B、（45°，90°）∪（90°，135°） |
| C、（0°，45°）∪（135°，180°） |
| D、（90°，135°） |
执行如图所示的程序框图，如果输入的N是195，则输出的P=（ ）
| A、11 | B、12 | C、13 | D、14 |
设奇函数f（x）在（0，+∞）上为单调递减函数，且f（2）=0，则不等式x•f（x）≤0的解集为（ ）
| A、（-∞，-2]∪（0，2] |
| B、[-2，0]∪[2，+∞） |
| C、（-∞，-2]∪[2，+∞） |
| D、[-2，0）∪（0，2] |
已知D是△ABC的边BC上（不包括B、C点）的一动点，且满足
=m
+n
，则
+
的最小值为（ ）
| AD |
| AB |
| AC |
| 1 |
| m |
| 2 |
| n |
| A、3 | ||
B、3+2
| ||
| C、4 | ||
D、4+2
|
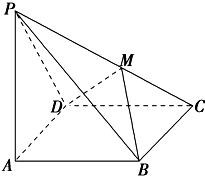如图所示，在四棱锥P-ABCD中，PA⊥底面ABCD，且底面各边都相等，∠DAB=60°，PA=AD=2，M是PC上的一动点．