题目内容
16.动圆P和圆C1:(x+1)2+y2=$\frac{1}{4}$外切和圆C2:(x-2)2+y2=$\frac{49}{4}$内切,那么动圆圆心P和已知两圆的圆心C1、C2构成三角形PC1C2的周长等于( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 由两圆的方程分别找出圆心C1与C2的坐标,及两圆的半径r1与r2,设圆P的半径为r,根据圆P与C1外切,得到圆心距PC1等于两半径相加,即PC1=r+$\frac{1}{2}$,又圆P与C2内切,得到圆心距PC2等于两半径相减,即PC2=$\frac{5}{2}$-r,由PC1+PC2等于常数2a,C1C2等于常数2c,可得出圆心P在焦点在x轴上,且长半轴为a,短半轴为b的椭圆上,即可得出结论.
解答 解:由圆C1:(x+1)2+y2=$\frac{1}{4}$和圆C2:(x-2)2+y2=$\frac{49}{4}$,
得到C1(-1,0),半径r1=$\frac{1}{2}$,C2(2,0),半径r2=$\frac{7}{2}$,
设圆P的半径为r,
∵圆P与C1外切而又与C2内切,
∴PC1=r+$\frac{1}{2}$,PC2=$\frac{7}{2}$-r,
∴PC1+PC2=(r+$\frac{1}{2}$)+($\frac{7}{2}$-r)=2a=4,又C1C2=2c=3,
∴a=2,c=1.5,
∴圆心P在焦点在x轴上,且长半轴为4的椭圆上
∴动圆圆心P和已知两圆的圆心C1、C2构成三角形PC1C2的周长等于2a+2c=7.
故选:C.
点评 此题考查了圆与圆的位置关系,椭圆的基本性质,以及动点的轨迹方程,两圆的位置关系由圆心角d与两圆半径R,r的关系来判断,当d<R-r时,两圆内含;当d=R-r时,两圆内切;当R-r<d<R+r时,两圆相交;当d=R+r时,两圆外切;当d>R+r时,两圆外离.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
4.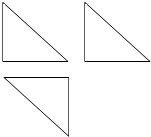 如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为( )
如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为( )
 如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为( )
如图,一个几何体的三视图是三个全等的等腰直角三角形,且直角边长为2,则这个几何体的外接球的表面积为( )| A. | 16π | B. | 12π | C. | 8π | D. | 4π |
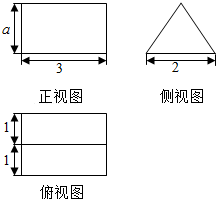 如图是一个几何体的三视图,若它的体积是3$\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.
如图是一个几何体的三视图,若它的体积是3$\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.