题目内容
19. 如图,在四棱锥E-ABCD中,EC⊥底面ABCD,AB⊥BC,AB∥CD,AB=1,CB=CD=CE=3.
如图,在四棱锥E-ABCD中,EC⊥底面ABCD,AB⊥BC,AB∥CD,AB=1,CB=CD=CE=3.(1)若F在侧棱DE上,且DF=2FE,求证:AF∥平面BCE;
(2)求平面ADE与平面BCE所成锐二面角的余弦值.
分析 由已知可得CB,CE,CD两两垂直,可以C为原点,建立如图的空间直角坐标系C-xyz,则C(0,0,0),D(3,0,0),B(0,3,0),E(0,0,3),F(1,0,2).A(1,3,0),利用向量法求解.
解答 解:∵EC⊥底面ABCD,AB⊥BC,AB∥CD,∴CB,CE,CD两两垂直,
故以C为原点,建立如图的空间直角坐标系C-xyz,则C(0,0,0),
D(3,0,0),B(0,3,0),E(0,0,3),F(1,0,2).A(1,3,0),
(1)证明:易得平面BCE的法向量为$\overrightarrow{m}=(1,0,0)$,$\overrightarrow{AF}=(0,-3,2)$
∵$\overrightarrow{m}•\overrightarrow{AF}=1×0+0×(-3)+0×2=0$,∴$\overrightarrow{AF}⊥\overrightarrow{m}$,
又AF?平面BCE,∴AF∥平面BCE;
(2)$\overrightarrow{AD}=(2,-3,0)$,$\overrightarrow{AE}=(-1,-3,3)$
设平面ADE的法向量为$\overrightarrow{n}=(x,y,z)$
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AD}=2x-3y=0}\\{\overrightarrow{n}•\overrightarrow{AE}=-x-3y+3z=0}\end{array}\right.$,可取$\overrightarrow{n}=(3,2,3)$
cos$<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{3}{1×\sqrt{22}}$=$\frac{3\sqrt{22}}{22}$
∴平面ADE与平面BCE所成锐二面角的余弦值为$\frac{3\sqrt{22}}{22}$.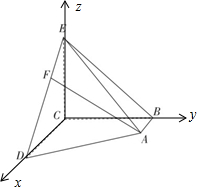
点评 本题考查了向量法求证线面平行、向量法求二面角,属于中档题.

 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案| A. | $\frac{{20\sqrt{5}}}{3}π$ | B. | $\frac{{64\sqrt{2}}}{3}π$ | C. | 20π | D. | 32π |
| A. | $\frac{\sqrt{13}}{13}$ | B. | $\frac{\sqrt{13}}{26}$ | C. | $\frac{\sqrt{13}}{52}$ | D. | $\frac{\sqrt{26}}{52}$ |
| x(小时) | 2 | 3 | 4 | 5 |
| y(个) | 1 | 2 | 4 | 5 |
(2)试预测加工8个零件需要多少时间.
| A. | ac<bc | B. | ca>cb | C. | logac>logbc | D. | logca>logcb |
| A. | -4 | B. | 4 | C. | $\frac{1}{4}$ | D. | $\frac{1}{9}{log_3}2$ |