题目内容
11.已知函数 f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x,x>0}\\{{2}^{x},x≤0}\end{array}\right.$,则 f(f($\frac{1}{9}$))的值为( )| A. | -4 | B. | 4 | C. | $\frac{1}{4}$ | D. | $\frac{1}{9}{log_3}2$ |
分析 先求出f($\frac{1}{9}$)=$lo{g}_{3}\frac{1}{9}$=-2,从而f(f($\frac{1}{9}$))=f(-2),由此能求出结果.
解答 解:∵函数 f(x)=$\left\{\begin{array}{l}{lo{g}_{3}x,x>0}\\{{2}^{x},x≤0}\end{array}\right.$,
∴f($\frac{1}{9}$)=$lo{g}_{3}\frac{1}{9}$=-2,
f(f($\frac{1}{9}$))=f(-2)=2-2=$\frac{1}{4}$.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.执行如图的程序框图,输出的结果为( )


| A. | 266 | B. | 268 | C. | 136 | D. | 134 |
6.若集合M={y|y=2017x},S={x|y=log2017(x-1)},则下列结论正确的是( )
| A. | M=S | B. | M∩S=∅ | C. | M∪S=S | D. | M∪S=M |
16.已知a,b∈R,i是虚数单位,若a-i与2+bi互为共轭复数,则a+bi在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,在四棱锥E-ABCD中,EC⊥底面ABCD,AB⊥BC,AB∥CD,AB=1,CB=CD=CE=3.
如图,在四棱锥E-ABCD中,EC⊥底面ABCD,AB⊥BC,AB∥CD,AB=1,CB=CD=CE=3. 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表)为( )
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表)为( ) 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系, 已知点
轴的非负半轴为极轴建立极坐标系, 已知点 的极坐标为
的极坐标为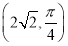 ,曲线
,曲线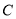 的参数方程为
的参数方程为 为参数).
为参数). 过
过 与点
与点 轴对称, 求曲线
轴对称, 求曲线