题目内容
1.已知P是△ABC内一点,$\overrightarrow{AP}$=$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AC}$,△PAC的面积为2016,则△PAB的面积为4032.分析 设$\overrightarrow{AM}=\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{AN}=\frac{1}{2}\overrightarrow{AC}$,以AM,AN为邻边作平行四边形AMPN,则根据线段的关系得出三角形的面积关系.
解答 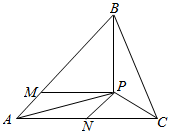 解:设$\overrightarrow{AM}=\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{AN}=\frac{1}{2}\overrightarrow{AC}$,以AM,AN为邻边作平行四边形AMPN,
解:设$\overrightarrow{AM}=\frac{1}{4}\overrightarrow{AB}$,$\overrightarrow{AN}=\frac{1}{2}\overrightarrow{AC}$,以AM,AN为邻边作平行四边形AMPN,
则S△AMP=$\frac{1}{4}$S△ABP,S△ANP=$\frac{1}{2}{S}_{△APC}$
∵S△AMP=S△ANP,
∴S△PAB=2S△PAC=4032.
故答案为:4032.
点评 本题考查了向量加减运算的性质和几何意义,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知全集U=R,集合A={-l,0,l,2},B={y|y=2x},图中阴影部分所表示的集合为( )


| A. | {-1,0} | B. | {l,2} | C. | {-l} | D. | {0,1,2} |
12.设集合A={x|x2-x=0},B={x|lnx<0},则A∪B=( )
| A. | (0,1] | B. | [0,1) | C. | (-∞,1] | D. | [0,1] |
9.函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,则f($\frac{2π}{3}$)=( )
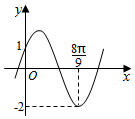

| A. | $\sqrt{3}$ | B. | 1 | C. | -1 | D. | -$\sqrt{3}$ |
11.($\sqrt{x}$+$\frac{1}{x}$)10的展开式含x的整数幂的项数为( )
| A. | 0 | B. | 2 | C. | 4 | D. | 6 |