题目内容
12．设集合A={x|x2-x=0}，B={x|lnx＜0}，则A∪B=（ ）| A． | （0，1] | B． | [0，1） | C． | （-∞，1] | D． | [0，1] |
分析 求出A中方程的解确定出A，求出B中不等式的解集确定出B，找出两集合的并集即可．
解答 解：由A中方程变形得：x（x-1）=0，
解得：x=0或x=1，即A={0，1}，
由B中不等式变形得：lnx＜0=ln1，即0＜x＜1，
∴B=（0，1），
则A∪B=[0，1]，
故选：D．
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
2．设函数f（x）=$\left\{\begin{array}{l}{2^{1-x}}，x≤1\\ 1-{log_2}x，x＞1\end{array}$，则f[f（-1）]=（ ）
| A． | -1 | B． | 1 | C． | -2 | D． | 2 |
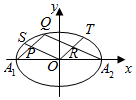如图，A1，A2为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的长轴的左、右端点，O为坐标原点，S，Q，T为椭圆上不同于A1，A2的三点，直线QA1，QA2，OS围成一个平行四边形OPQR，则|OS|2+|OT|2=（ ）