Question

若函数f（x）=

1

4

sin（πx）与函数g（x）=x³+bx+c的定义域为[0，2]，它们在同一点有相同的最小值，则b+c=

 

．

Answer 1

考点：利用导数求闭区间上函数的最值

专题：导数的综合应用

分析：先画出函数f（x）的图象，得到x=

3

2

时，f（x）的最小值是-

1

4

，求出函数g（x）的导数，分别将（

3

2

，0）代入导函数，（

3

2

，-

1

4

）代入函数的表达式，求出b，c的值，得到答案．

解答： 解：画出函数f（x）的图象，如图示：
，
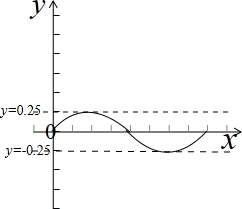当x=

3

2

时，f（x）取到最小值-

1

4

，
此时：g′（

3

2

）=3×(

3

2

)2+b=0，解得：b=-

27

4

，
g（

3

2

）=(

3

2

)3+（-

27

4

）×

3

2

+c=-

1

4

，解得：c=

13

2

，
∴b+c=-

1

4

，
故答案为：-

1

4

．

点评：本题考查了函数的最值问题，考查了三角函数的图象及性质，考查导数的应用，是一道中档题．