题目内容
3.点M(20,40),抛物线y2=2px(p>0)的焦点为F,若对于抛物线上的任意点P,|PM|+|PF|的最小值为41,则p的值等于42或22.分析 过P做抛物线的准线的垂线,垂足为D,则|PF|=|PD|,当M(20,40)位于抛物线内,当M,P,D共线时,|PM|+|PF|的距离最小,20+$\frac{p}{2}$=41,解得:p=42,当M(20,40)位于抛物线外,由勾股定理可知:$\sqrt{4{0}^{2}+(20-\frac{p}{2})^{2}}$=41,p=22或58,当p=58时,y2=116x,则点M(20,40)在抛物线内,舍去,即可求得p的值.
解答 解:由抛物线的定义可知:抛物线上的点到焦点距离=到准线的距离,
过P做抛物线的准线的垂线,垂足为D,则|PF|=|PD|,
当M(20,40)位于抛物线内,
∴|PM|+|PF|=|PM|+|PD|,
当M,P,D共线时,|PM|+|PF|的距离最小,
由最小值为41,即20+$\frac{p}{2}$=41,解得:p=42,
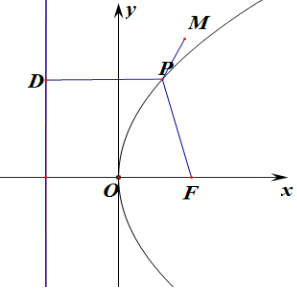
当M(20,40)位于抛物线外,
当P,M,F共线时,|PM|+|PF|取最小值,
即$\sqrt{4{0}^{2}+(20-\frac{p}{2})^{2}}$=41,解得:p=22或58,
由当p=58时,y2=116x,则点M(20,40)在抛物线内,舍去,
故答案为:42或22.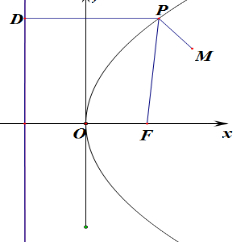
点评 本题考查抛物线的标准方程,抛物线的定义的应用,考查计算能力,属于中档题.

练习册系列答案
相关题目
13.已知平面α内有一点M(1,-1,2),平面α的一个法向量$\overrightarrow n$=(2,-1,2),则下列点P在平面α内的是( )
| A. | (-4,4,0) | B. | (2,0,1) | C. | (2,3,3) | D. | (3,-3,4) |
14.设a∈R,则“a=1”是“复数(a-1)(a+2)+(a+3)i为纯虚数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |