题目内容
2.已知f(x)=ax-blnx,曲线y=f(x)在点(1,f(1))处的切线方程为y=x+1.(1)求函数f(x)单调区间;
(2)对任意x≥1,f(x)≥kx恒成立,求k的取值范围.
分析 (1)求出函数的导数,得到关于a,b的方程组,求出a,b的值,求出函数的单调区间即可;
(2)问题转化为k≤2-$\frac{lnx}{x}$在x≥1时恒成立,设g(x)=2-$\frac{lnx}{x}$,x≥1,根据函数的单调性求出k的范围即可.
解答 解:(1)由题意得:f′(x)=a-$\frac{b}{x}$,(x>0),
而曲线y=f(x)在点(1,f(1))处的切线方程为y=x+1,
故$\left\{\begin{array}{l}{f(1)=2}\\{f′(1)=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$,
∴f′(x)=2-$\frac{1}{x}$=$\frac{2x-1}{x}$,(x>0),
令f′(x)>0,解得:x>$\frac{1}{2}$,令f′(x)<0,解得:0<x<$\frac{1}{2}$,
∴f(x)在($\frac{1}{2}$,+∞)递增,在(0,$\frac{1}{2}$)递减;
(2)由(1)得:f(x)=2x-lnx,
∴f(x)≥kx即k≤2-$\frac{lnx}{x}$在x≥1时恒成立,
设g(x)=2-$\frac{lnx}{x}$,x≥1,
则g′(x)=$\frac{lnx-1}{{x}^{2}}$,
∴g(x)在(e,+∞)递增,在[1,e)递减,
故x=e时,g(x)有最小值2-$\frac{1}{e}$,
∴k≤2-$\frac{1}{e}$.
点评 本题考查了求出方程问题,考查函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
相关题目
12.已知{an}是公差为1的等差数列,Sn为{an}的前n项和,若S6=4S3,则a10=( )
| A. | $\frac{17}{2}$ | B. | $\frac{19}{2}$ | C. | $\frac{9}{10}$ | D. | $\frac{8}{9}$ |
10.若某个扇形的半径为3cm,弧长为πcm,则该扇形的面积为( )
| A. | πcm2 | B. | $\frac{3}{2}π$cm2 | C. | 3πcm2 | D. | 6πcm2 |
17.若f(x)=sinα-cosx,则f′(x)等于( )
| A. | 2sinα+cosx | B. | cosα+sinx | C. | cosx | D. | sinx |
14.已知两正数x,y 满足x+y=1,则z=$(x+\frac{1}{x})(y+\frac{1}{y})$的最小值为( )
| A. | $\frac{33}{4}$ | B. | $\frac{25}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{{\sqrt{17}}}{4}$ |
11.a、b均为实数,则a<b<0是a2>b2的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
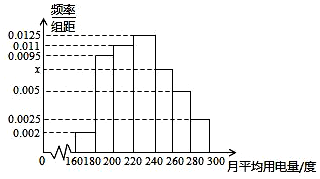 某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图示.