题目内容
19.在平面直角坐标系xOy中,已知点A(1,-2),B(-2,3),C(2,-1),以线段AB,AC为邻边作平行西变形ABDC.(Ⅰ)求平行四边形ABDC两条对角线所成的角(非钝角)的余弦值;
(Ⅱ)设实数t满足($\overrightarrow{AB}$-t$\overrightarrow{OC}$)⊥$\overrightarrow{OD}$=0,求t的值.
分析 (I)由已知可得:$\overrightarrow{AD}$=$\overrightarrow{AB}+\overrightarrow{AC}$,$\overrightarrow{CB}$=$\overrightarrow{AB}-\overrightarrow{AC}$,利用cos$<\overrightarrow{AC},\overrightarrow{CB}>$=$\frac{\overrightarrow{AD}•\overrightarrow{CB}}{|\overrightarrow{AD}||\overrightarrow{CB}|}$即可得出.
(Ⅱ)$\overrightarrow{AD}=\overrightarrow{OD}-\overrightarrow{OA}$,可得$\overrightarrow{OD}$,$\overrightarrow{AB}$-t$\overrightarrow{OC}$=(-3-2t,5+t),根据实数t满足($\overrightarrow{AB}$-t$\overrightarrow{OC}$)⊥$\overrightarrow{OD}$=0,可得($\overrightarrow{AB}$-t$\overrightarrow{OC}$)•$\overrightarrow{OD}$=0.
解答 解:(I)由已知可得:$\overrightarrow{AB}$=(-3,5),$\overrightarrow{AC}$=(1,1),
则$\overrightarrow{AD}$=$\overrightarrow{AB}+\overrightarrow{AC}$=(-2,6),$\overrightarrow{CB}$=$\overrightarrow{AB}-\overrightarrow{AC}$=(-4,4).
∴$|\overrightarrow{AD}|$=2$\sqrt{10}$,$|\overrightarrow{CB}|$=4$\sqrt{2}$,
cos$<\overrightarrow{AC},\overrightarrow{CB}>$=$\frac{\overrightarrow{AD}•\overrightarrow{CB}}{|\overrightarrow{AD}||\overrightarrow{CB}|}$=$\frac{32}{2\sqrt{10}×4\sqrt{2}}$=$\frac{2\sqrt{5}}{5}$.
∴平行四边形ABDC两条对角线所成的角(非钝角)的余弦值为$\frac{2\sqrt{5}}{5}$.
(Ⅱ)$\overrightarrow{AD}=\overrightarrow{OD}-\overrightarrow{OA}$=(-2,6),∴$\overrightarrow{OD}$=$\overrightarrow{OA}+(-2,6)$=(-1,4),又$\overrightarrow{OC}$=(2,-1),
∴$\overrightarrow{AB}$-t$\overrightarrow{OC}$=(-3-2t,5+t),
∵实数t满足($\overrightarrow{AB}$-t$\overrightarrow{OC}$)⊥$\overrightarrow{OD}$=0,∴($\overrightarrow{AB}$-t$\overrightarrow{OC}$)•$\overrightarrow{OD}$=6t+23=0,
∴t=-$\frac{23}{6}$.
点评 本题考查了向量坐标运算性质、向量夹角公式、向量垂直与数量积的关系、模的计算公式,考查了推理能力与计算能力,属于中档题.

| A. | 3x-y+8=0 | B. | x-3y+8=0 | C. | 3x+y+8=0 | D. | 3x+y+4=0 |

| A. | a>0,c<0,d>0 | B. | a>0,c>0,d<0 | C. | a<0,c<0,d<0 | D. | a<0,c>0,d<0 |
| A. | 2 | B. | $2+\sqrt{2}$ | C. | $2+\sqrt{3}$ | D. | $2-\sqrt{2}$ |
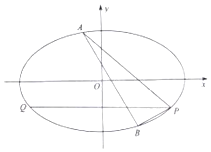 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,并且过点P(2,-1)
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,并且过点P(2,-1)