题目内容
已知函数f(x)=lnx-kx+1(k∈R)
(Ⅰ)当k=1时,求函数f(x)的单调区间;
(Ⅱ)若f(x)≤0恒成立,试确定实数k的取值范围;
(Ⅲ)证明:
+
+
+…+
<
(n∈N*且n>1)
(Ⅰ)当k=1时,求函数f(x)的单调区间;
(Ⅱ)若f(x)≤0恒成立,试确定实数k的取值范围;
(Ⅲ)证明:
| ln2 |
| 3 |
| ln3 |
| 4 |
| ln4 |
| 5 |
| lnn |
| n+1 |
| n(n-1) |
| 4 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由函数f(x)的定义域为(0,+∞),f′(x)=
-1.能求出函数f(x)的单调区间.
(Ⅱ)由(1)知k≤0时,f(x)在(0,+∞)上是增函数,而f(1)=1-k>0,f(x)≤0不成立,故k>0,又由(1)知f(x)的最大值为f(
),由此能确定实数k的取值范围.
(Ⅲ)由(2)知,当k=1时,有f(x)≤0在(0,+∞)恒成立,且f(x)在(1,+∞)上是减函数,f(1)=0,即lnx<x-1在x∈[2,+∞)上恒成立,由此能够证明
+
+
+…+
<
(n∈N*且n>1)
| 1 |
| x |
(Ⅱ)由(1)知k≤0时,f(x)在(0,+∞)上是增函数,而f(1)=1-k>0,f(x)≤0不成立,故k>0,又由(1)知f(x)的最大值为f(
| 1 |
| k |
(Ⅲ)由(2)知,当k=1时,有f(x)≤0在(0,+∞)恒成立,且f(x)在(1,+∞)上是减函数,f(1)=0,即lnx<x-1在x∈[2,+∞)上恒成立,由此能够证明
| ln2 |
| 3 |
| ln3 |
| 4 |
| ln4 |
| 5 |
| lnn |
| n+1 |
| n(n-1) |
| 4 |
解答:
解:(Ⅰ)易知f(x)的定义域为(0,+∞),
又f′(x)=
-1
当0<x<1时,f′(x)>0;
当x>1时,f′(x)<0
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数.
(Ⅱ)当k≤0时,f(1)=1-k>0,不成立,
故只考虑k>0的情况
又f′(x)=
-k
当k>0时,当0<x<
时,f′(x)>0;
当x>
时,f′(x)<0
在(0,
)上是增函数,在(
,+∞)时减函数,
此时f(x)max=f(
)=-lnk
要使f(x)≤0恒成立,只要-lnk≤0 即可
解得:k≥1.
(Ⅲ)当k=1时,
有f(x)≤0在(0,+∞)恒成立,
且f(x)在(1,+∞)上是减函数,f(1)=0,
即lnx<x-1在x∈(1,+∞)上恒成立,
令x=n2,则lnn2<n2-1,
即2lnn<(n-1)(n+1),
∴
<
(n∈N*且n>1)
∴
+
+
+…+
<
+
+
+…+
=
即:
+
+
+…+
<
(n∈N*且n>1)成立.
又f′(x)=
| 1 |
| x |
当0<x<1时,f′(x)>0;
当x>1时,f′(x)<0
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数.
(Ⅱ)当k≤0时,f(1)=1-k>0,不成立,
故只考虑k>0的情况
又f′(x)=
| 1 |
| x |
当k>0时,当0<x<
| 1 |
| k |
当x>
| 1 |
| k |
在(0,
| 1 |
| k |
| 1 |
| k |
此时f(x)max=f(
| 1 |
| k |
要使f(x)≤0恒成立,只要-lnk≤0 即可
解得:k≥1.
(Ⅲ)当k=1时,
有f(x)≤0在(0,+∞)恒成立,
且f(x)在(1,+∞)上是减函数,f(1)=0,
即lnx<x-1在x∈(1,+∞)上恒成立,
令x=n2,则lnn2<n2-1,
即2lnn<(n-1)(n+1),
∴
| lnn |
| n+1 |
| n-1 |
| 2 |
∴
| ln2 |
| 3 |
| ln3 |
| 4 |
| ln4 |
| 5 |
| lnn |
| n+1 |
| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 2 |
| n-1 |
| 2 |
| n(n-1) |
| 4 |
即:
| ln2 |
| 3 |
| ln3 |
| 4 |
| ln4 |
| 5 |
| lnn |
| n+1 |
| n(n-1) |
| 4 |
点评:本题考查函数单调区间的求法,确定实数的取值范围,不等式的证明.考查化归与转化、分类与整合的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

练习册系列答案
相关题目
把函数y=sinx(x∈R)的图象上所有点向左平行移动
个单位长度,再把所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象所表示的函数是( )
| π |
| 3 |
A、y=sin(
| ||||
B、y=sin(
| ||||
C、y=sin(2x-
| ||||
D、y=sin(2x+
|
如图1是某学习小组学生数学考试成绩的茎叶图,1号到16号同学的成绩依次为A1,A2,…,A16,图2是茎叶图中成绩在一定范围内的学生人数的算法流程图,那么该算法流程图输出的结果是( )
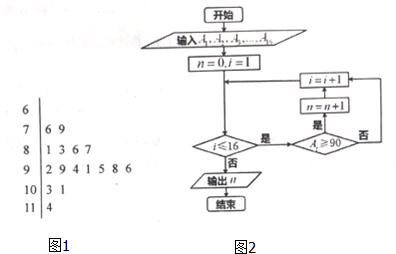

| A、6 | B、10 | C、91 | D、92 |
下列命题说法错误的是( )
| A、若“p∧q”为真命题,则p,q均为真命题 | ||||
| B、若命题p:?x∈R,x2≥0,则¬p:?x∈R,x2<0 | ||||
| C、“x>2”是“x≥0”的充分不必要条件 | ||||
D、“x=
|
已知点O为坐标原点,点A(1,0,0)、点B(1,1,0),则下列各向量中是平面AOB的一个法向量的是( )
| A、(1,1,1) |
| B、(1,0,1) |
| C、(0,1,1) |
| D、(0,0,1) |
设扇形的周长为8cm,面积为4cm2,则扇形的圆心角是( )rad.
| A、1 | B、2 | C、π | D、1或2 |
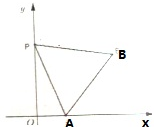 如图在平面内放置的边长为1的正三角形PAB沿x轴滚动,设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为
如图在平面内放置的边长为1的正三角形PAB沿x轴滚动,设顶点P(x,y)的轨迹方程是y=f(x),则f(x)的最小正周期为