题目内容
下列命题说法错误的是( )
| A、若“p∧q”为真命题,则p,q均为真命题 | ||||
| B、若命题p:?x∈R,x2≥0,则¬p:?x∈R,x2<0 | ||||
| C、“x>2”是“x≥0”的充分不必要条件 | ||||
D、“x=
|
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.利用复合命题真假的判断方法即可得出正误;
B.利用复合命题真假的判断方法即可得出正误;
C.“x>2”⇒“x≥0”,反之不成立,即可判断出;
D.“x=
”是“sinx=
”的充分不必要条件,即可判断出正误.
B.利用复合命题真假的判断方法即可得出正误;
C.“x>2”⇒“x≥0”,反之不成立,即可判断出;
D.“x=
| π |
| 6 |
| 1 |
| 2 |
解答:
解:A.“p∧q”为真命题,则p,q均为真命题,正确;
B.命题p:?x∈R,x2≥0,则¬p:?x∈R,x2<0,正确;
C.“x>2”⇒“x≥0”,反之不成立,例如x=1时,满足x≥0,但是x<2,因此“x>2”是“x≥0”的充分不必要条件,正确;
D.“x=
”⇒“sinx=
”,反之不成立,因此“x=
”是“sinx=
”的此充分不必要条件,不正确.
故选:D.
B.命题p:?x∈R,x2≥0,则¬p:?x∈R,x2<0,正确;
C.“x>2”⇒“x≥0”,反之不成立,例如x=1时,满足x≥0,但是x<2,因此“x>2”是“x≥0”的充分不必要条件,正确;
D.“x=
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
故选:D.
点评:本题考查了简易逻辑的判定方法,考查了推理能力,属于基础题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、命题“若p或q”为真命题,则p,q中至少有一个为真命题 |
| B、命题“?x0∈R,x02+x0-1<0”的否定是“?x∈R,x2+x-1>0” |
| C、命题“若x=y,则sinx=siny”的逆否命题为假命题 |
| D、命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” |
已知-
<α<β<
,则α-β的范围是( )
| π |
| 6 |
| 2π |
| 3 |
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-
|
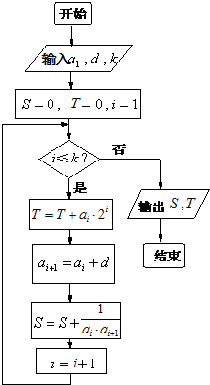 如图所示,程序框图给出了无穷正项数列{an}满足的条件,且当k=5时,输出的S是
如图所示,程序框图给出了无穷正项数列{an}满足的条件,且当k=5时,输出的S是