题目内容
12.30岁以后,随着年龄的增长,人们的身体机能在逐渐退化,所以打针 买保健品这样的“健康消费”会越来越多,现对某地区不同年龄段的一些人进行了调查,得到其一年内平均“健康消费”如表:| 年龄(岁) | 30 | 35 | 40 | 45 | 50 |
| 健康消费(百元) | 5 | 8 | 10 | 14 | 18 |
(2)由(1)所得方程,估计该地区的人在60岁时的平均“健康消费”.
(附:线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,其中$\overline{x}$,$\overline{y}$为样本平均值)
分析 (1)求出回归系数,即可求“健康消费”y关于年龄x的线性回归方程;
(2)由(1)所得方程,代入计算,估计该地区的人在60岁时的平均“健康消费”.
解答 解:(1)由题意,$\overline{x}$=50,$\overline{y}$=11,
∴$\widehat{b}$=$\frac{150+280+400+630+900-5×50×11}{900+1225+1600+2025+2500-5×2500}$=$\frac{39}{425}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=$\frac{109}{17}$,
∴$\widehat{y}$=$\frac{39}{425}$x+$\frac{109}{17}$;
(2)x=60时,$\widehat{y}$=$\frac{39}{425}$×60+$\frac{109}{17}$≈12.
点评 本题考查回归方程,考查学生的计算能力,正确求出回归系数是关键.

练习册系列答案
相关题目
7.圆x2+y2=1与直线xsinθ+y-1=0的位置关系为( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 相切或相交 |
4.已知集合$A=\left\{{x\left|{\frac{x-1}{x+3}>0}\right.}\right\}$,$B=\left\{{y\left|{y=\sqrt{4-{x^2}}}\right.}\right\}$,则A∪B=( )
| A. | (-∞,-3)∪(1,+∞) | B. | (-∞,-3)∪(1,2] | C. | (-∞,-3)∪[0,+∞) | D. | (1,2] |
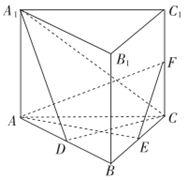 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.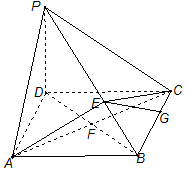 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是 菱形,AC=6,$BD=6\sqrt{3}$,E是PB上任意一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是 菱形,AC=6,$BD=6\sqrt{3}$,E是PB上任意一点. 如图,D是△ABC内一点,角A,B,C的对边分别是a,b,c,且满足∠D=2∠B,cos∠D=-$\frac{1}{3}$,AD=2,△ACD的面积是4$\sqrt{2}$.
如图,D是△ABC内一点,角A,B,C的对边分别是a,b,c,且满足∠D=2∠B,cos∠D=-$\frac{1}{3}$,AD=2,△ACD的面积是4$\sqrt{2}$.