题目内容
8.设a,b∈R,c∈[0,2π),若对任意实数x都有2sin(3x-$\frac{π}{3}$)=asin(bx+c),则满足条件的a,b,c的组数为( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
分析 由题意确定a,b,从而可得满足条件的a,b,c的组数.
解答 解:由题意2sin(3x-$\frac{π}{3}$)=asin(bx+c),他们周期和最值相同,
∵sin(bx+c)在b∈R,c∈[0,2π)的值可以取得±1,
∴a=±2.
同理:对任意实数x都成立,他们周期相同,∴b=±3.
那么c∈[0,2π)只有唯一的值与其对应.
∴满足条件的a,b,c的组数为4组.
故选:D.
点评 本题考查了三角函数的性质的灵活运用.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知指数函数$f(x)={(\frac{1}{2})^x}$,则使得f(m)>1成立的实数m的取值范围是( )
| A. | (1,+∞) | B. | (0,+∞) | C. | (-∞,1) | D. | (-∞,0) |
19.利用计算器,列出自变量和函数值的对应值如表:
那么方程2x=x2有一个根位于下列区间的( )
| x | -1.6 | -1.4 | -1.2 | -1 | -0.8 | -0.6 | -0.4 | -0.2 | 0 | … |
| y=2x | 0.3299 | 0.3789 | 0.4353 | 0.5 | 0.5743 | 0.6598 | 0.7579 | 0.8706 | 1 | … |
| y=x2 | 2.56 | 1.96 | 1.44 | 1 | 0.64 | 0.36 | 0.16 | 0.04 | 0 | … |
| A. | (-1.6,-1.2) | B. | (-1.2,-0.8) | C. | (-0.8,-0.6) | D. | (-0.6,-0.2) |
18.圆心在x+y=0上,且与x轴交于点A(-3,0)和B(1,0)的圆的方程为( )
| A. | (x+1)2+(y-1)2=5 | B. | (x-1)2+(y+1)2=$\sqrt{5}$ | C. | (x-1)2+(y+1)2=5 | D. | (x+1)2+(y-1)2=$\sqrt{5}$ |
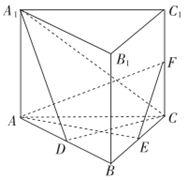 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.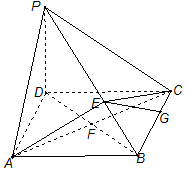 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是 菱形,AC=6,$BD=6\sqrt{3}$,E是PB上任意一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是 菱形,AC=6,$BD=6\sqrt{3}$,E是PB上任意一点. 如图,D是△ABC内一点,角A,B,C的对边分别是a,b,c,且满足∠D=2∠B,cos∠D=-$\frac{1}{3}$,AD=2,△ACD的面积是4$\sqrt{2}$.
如图,D是△ABC内一点,角A,B,C的对边分别是a,b,c,且满足∠D=2∠B,cos∠D=-$\frac{1}{3}$,AD=2,△ACD的面积是4$\sqrt{2}$.