题目内容
14.设集合A={x|x2+3x+2=0},B={x|x2+ax+4=0},若B≠Φ,B⊆A,则实数a的取值集合是{4}.分析 化简集合A,根据B⊆A,B≠Φ建立条件关系即可求实数a的取值.
解答 解:集合A={x|x2+3x+2=0}={-1,-2},
B={x|x2+ax+4=0},
∵B⊆A,且B≠Φ,即方程x2+ax+4=0有解.
那么:x=-1是方程x2+ax+4=0的解.
可得a=5,此时方程为x2+5x+4=0,另一个解x=4,不满足题意.
当x=-2是方程x2+ax+4=0的解,
可得a=4,此时方程为x2+4x+4=0,只有一个解,满足题意.
故答案为:{4}.
点评 本题主要考查集合的基本运算,比较基础

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
9.设M={α|α=k•90°,k∈Z}∪{α|α=k•180°+45°,k∈Z},N={α|α=k•45°,k∈Z},则( )
| A. | M⊆N | B. | M?N | C. | M=N | D. | M∩N=Φ |
19.利用计算器,列出自变量和函数值的对应值如表:
那么方程2x=x2有一个根位于下列区间的( )
| x | -1.6 | -1.4 | -1.2 | -1 | -0.8 | -0.6 | -0.4 | -0.2 | 0 | … |
| y=2x | 0.3299 | 0.3789 | 0.4353 | 0.5 | 0.5743 | 0.6598 | 0.7579 | 0.8706 | 1 | … |
| y=x2 | 2.56 | 1.96 | 1.44 | 1 | 0.64 | 0.36 | 0.16 | 0.04 | 0 | … |
| A. | (-1.6,-1.2) | B. | (-1.2,-0.8) | C. | (-0.8,-0.6) | D. | (-0.6,-0.2) |
6.已知集合A={x|(x+1)(x-2)>0},B={x∈Z|x2-9≤0},则A∩B=( )
| A. | {0,1} | B. | (0,1) | C. | [-3,-1)∪(2,3] | D. | {-3,-2,3} |
4.已知集合$A=\left\{{x\left|{\frac{x-1}{x+3}>0}\right.}\right\}$,$B=\left\{{y\left|{y=\sqrt{4-{x^2}}}\right.}\right\}$,则A∪B=( )
| A. | (-∞,-3)∪(1,+∞) | B. | (-∞,-3)∪(1,2] | C. | (-∞,-3)∪[0,+∞) | D. | (1,2] |
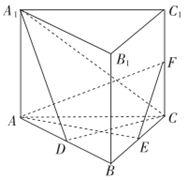 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.