题目内容
已知与圆C:x2+y2-2x-2y+1=0相切的直线l交x轴,y轴于A,B两点,|OA|=a,|OB|=b(a>2,b>2).
(Ⅰ)求证:(a-2)(b-2)=2;
(Ⅱ)求线段AB中点的轨迹方程;
(Ⅲ)求△AOB面积的最小值.
(Ⅰ)求证:(a-2)(b-2)=2;
(Ⅱ)求线段AB中点的轨迹方程;
(Ⅲ)求△AOB面积的最小值.
考点:直线和圆的方程的应用,圆方程的综合应用
专题:综合题,直线与圆
分析:(Ⅰ)设直线方程,利用圆心到该直线的距离等于半径,建立方程,化简可得结论;
(Ⅱ)设AB中点M(x,y),则a=2x,b=2y,利用代入法,即可得出结论;
(Ⅲ)由(a-2)(b-2)=2得ab+2=2(a+b)≥4
,结合三角形的面积公式,可求△AOB面积的最小值.
(Ⅱ)设AB中点M(x,y),则a=2x,b=2y,利用代入法,即可得出结论;
(Ⅲ)由(a-2)(b-2)=2得ab+2=2(a+b)≥4
| ab |
解答:
(Ⅰ)证明:圆的标准方程是(x-1)2+(y-1)2=1,
设直线方程为
+
=1,即bx+ay-ab=0,
所以圆心到该直线的距离d=
=1,
即a2+b2+a2b2+2ab-2a2b-2ab2=a2+b2,
即a2b2+2ab-2a2b-2ab2=0,
即ab+2-2a-2b=0,即(a-2)(b-2)=2.
(Ⅱ)解:设AB中点M(x,y),则a=2x,b=2y,
代入(a-2)(b-2)=2,得(x-1)(y-1)=
(x>1,y>1).
(Ⅲ)解:由(a-2)(b-2)=2得ab+2=2(a+b)≥4
,
解得
≥2+
(舍去
≤2-
),
当且仅当a=b时,ab取最小值6+4
,
所以△AOB面积的最小值是3+2
.
设直线方程为
| x |
| a |
| y |
| b |
所以圆心到该直线的距离d=
| |a+b-ab| | ||
|
即a2+b2+a2b2+2ab-2a2b-2ab2=a2+b2,
即a2b2+2ab-2a2b-2ab2=0,
即ab+2-2a-2b=0,即(a-2)(b-2)=2.
(Ⅱ)解:设AB中点M(x,y),则a=2x,b=2y,
代入(a-2)(b-2)=2,得(x-1)(y-1)=
| 1 |
| 2 |
(Ⅲ)解:由(a-2)(b-2)=2得ab+2=2(a+b)≥4
| ab |
解得
| ab |
| 2 |
| ab |
| 2 |
当且仅当a=b时,ab取最小值6+4
| 2 |
所以△AOB面积的最小值是3+2
| 2 |
点评:本题考查直线与圆的位置关系,考查代入法求轨迹方程,考查基本不等式的运用,考查三角形面积的计算,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
若复数i满足z(1+i)=2i,则在复平面内z对应的点的坐标是( )
| A、(1,1) |
| B、(1,-1) |
| C、(-1,1) |
| D、(-1,-1) |
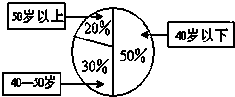 某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,…,196-200号).若第6组抽出的号码为28,则第8组抽出的号码应是a; 若用分层抽样方法,则50岁以下年龄段应抽取b人.那么a+b等于( )
某单位200名职工的年龄分布情况如图,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组(1-5号,6-10号,…,196-200号).若第6组抽出的号码为28,则第8组抽出的号码应是a; 若用分层抽样方法,则50岁以下年龄段应抽取b人.那么a+b等于( )