题目内容
已知函数f（x）在区间（a，b）有意义，x1，x2∈（a，b），使f（x1）＜0，f（x2）＞0，则称f（x）在（a，b）不保号，若函数f（x）=3x2+2（1-a）x-a（a+2）在区间（-1，1）不保号，求a的范围．
考点：二次函数的性质
专题：函数的性质及应用
分析：根据新定义对称f（-1）＜0，f（1）＞0，解不等式组求出a的范围即可．
解答：
解：由题意得：
，
即
，
解得：-5＜a＜-1，
∴a的范围是（-5，-1）．
|
即
|
解得：-5＜a＜-1，
∴a的范围是（-5，-1）．
点评：本题考查了二次函数的性质，考查新定义问题，是一道基础题．
练习册系列答案
名校课堂系列答案
相关题目
若函数f（x）=ax2-ln（2x+1）在区间[1，2]上为单调函数，则实数a不可能取到的值为（ ）
| A、1 | ||
B、
| ||
C、
| ||
D、
|
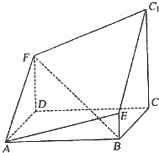如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的，其中AB=4，BC=2，CC1=3，BE=1