题目内容
6.给出下列四个命题:①如果两个命题互为逆否命题,那么它们的真假性相同;
②命题“若a,b都是偶数,则a+b是偶数”的否命题为真命题;
③已知点A(-1,0),B(1,0),若|PA|-|PB|=2,则动点P的轨迹为双曲线的一支;
④对于空间任意一点O和不共线的三点A,B,C,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$,则x+y+z=1是四点P,A,B,C共面的充要条件.
其中所有正确的命题的序号为①④.
分析 直接由互为逆否命题的两个命题共真假判断①;写出命题的否命题并判断真假判断②;由双曲线定义判断③;由共面向量基本定理可知④正确.
解答 解:由互为逆否命题的两个命题共真假可知命题①正确;
命题“若a,b都是偶数,则a+b是偶数”的否命题为:“若a,b不都是偶数,则a+b不是偶数”,是假命题.如a=1,b=3不都是偶数,但a+b=4是偶数;
已知点A(-1,0),B(1,0),若|PA|-|PB|=2,则动点P的轨迹为一条射线,故③错误;
由共面向量基本定理可知,对于空间任意一点O和不共线的三点A,B,C,若$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$+z$\overrightarrow{OC}$,则x+y+z=1是四点P,A,B,C共面的充要条件,故④正确.
故答案为:①④.
点评 本题考查命题的真假判断与应用,考查了命题的逆命题、否命题以及逆否命题的真假判断,考查双曲线的定义,考查共面向量基本定理及其应用,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.设函数f(x)=$\left\{\begin{array}{l}{2^{-x}}-1,{\;}^{\;}x≤0\\{x^{\frac{1}{2}}},{\;}^{\;}{\;}^{\;}x>0\end{array}$如果f(x0)>1,则x0的取值范围是( )
| A. | (-1,1) | B. | (-1,0)∪(1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
1.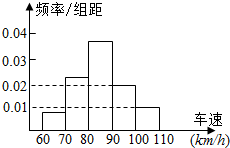 在某路段车辆检测点,随机抽取了400辆过往汽车进行车速检测,检测结果的频率分布直方图如图所示,则这400辆汽车中车速大于90km/h的汽车约有( )
在某路段车辆检测点,随机抽取了400辆过往汽车进行车速检测,检测结果的频率分布直方图如图所示,则这400辆汽车中车速大于90km/h的汽车约有( )
 在某路段车辆检测点,随机抽取了400辆过往汽车进行车速检测,检测结果的频率分布直方图如图所示,则这400辆汽车中车速大于90km/h的汽车约有( )
在某路段车辆检测点,随机抽取了400辆过往汽车进行车速检测,检测结果的频率分布直方图如图所示,则这400辆汽车中车速大于90km/h的汽车约有( )| A. | 12辆 | B. | 80辆 | C. | 100辆 | D. | 120辆 |
18.若f(x)=$\left\{\begin{array}{l}-2x-2,x∈({-∞,0})\\{x^2}-2x-1,x∈[0,+∞)\end{array}$,x1≤x2≤x3,且f(x1)=f(x2)=f(x3),则x1+x2+x3的取值的范围是( )
| A. | $[{\frac{3}{2},2})$ | B. | $[{\frac{3}{2},2}]$ | C. | $({-\frac{1}{2},1}]$ | D. | $[{\frac{1}{2},2})$ |