题目内容
16．已知f（x）=$\left\{\begin{array}{l}{{x}^{2}+4x，x≥0}\\{4x-{x}^{2}，x＜0}\end{array}\right.$，若f（a-2）+f（a）＞0，求a的取值范围．分析 先根据分段函数，得到函数的单调性与奇偶性，再根据单调性去掉“f”，解一元二次不等式可求出a的取值范围．
解答 解：由题意，函数f（x）=$\left\{\begin{array}{l}{{x}^{2}+4x，x≥0}\\{4x-{x}^{2}，x＜0}\end{array}\right.$在R上单调递增，且为奇函数．
而f（a-2）+f（a）＞0，
则a-2＞-a，解得a＞1．
点评 本题主要考查了分段函数的图象及其性质，以及一元二次不等式的解法，解题的关键判定函数的单调性，属于基础题．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
相关题目
6．已知函数f（x）=$\frac{1}{3}$ax3+$\frac{1}{2}$bx2+cx+d，其图象在点（1，f（1））处的切线斜率为0，若a＜b＜c，且函数f（x）的单调递增区间为（m，n），则n-m的取值范围是（ ）
| A． | （1，$\frac{3}{2}$） | B． | （$\frac{3}{2}$，3） | C． | （1，3） | D． | （2，3） |
7．直线l将圆x2+y2-2x-4y=0平分，且与直线$\frac{x}{2}$-$\frac{y}{4}$=1平行，则直线l的方程是（ ）
| A． | 2x-y-4=0 | B． | x+2y-3=0 | C． | 2x-y=0 | D． | x-2y+3=0 |
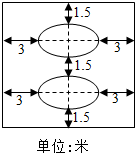某学校拟在广场上建造一个矩形花园，如图所示，中间是完全相同的两个椭圆型花坛，每个椭圆型花坛的面积均为216π平方米，两个椭圆花坛的距离是1.5米．整个矩形花坛的占地面积为S．