题目内容
一直线过点M(-3,
),且被圆x2+y2=25所截得的弦长为8,则此直线方程为 .
| 3 |
| 2 |
考点:直线与圆相交的性质
专题:直线与圆
分析:由题意可得弦心距为3,再分所求的直线的斜率存在和不存在两种情况,分别求得直线的方程.
解答:
解:圆x2+y2=25的圆心为原点(0,0),半径等于5,
当所求的直线的斜率不存在时,直线的方程为x=-3,弦心距为3,故弦长为8,满足条件.
当所求的直线的斜率存在时,设所求的直线的方程为y-
=k(x+3),即 2kx-2y+6k+3=0.
再根据弦心距d=
=3=
,求得 k=
,可得此时直线的方程为3x-4y+15=0,
故答案为:x=-3,3x-4y+15=0.
当所求的直线的斜率不存在时,直线的方程为x=-3,弦心距为3,故弦长为8,满足条件.
当所求的直线的斜率存在时,设所求的直线的方程为y-
| 3 |
| 2 |
再根据弦心距d=
| 52-42 |
| |0-0+6k+3| | ||
|
| 3 |
| 4 |
故答案为:x=-3,3x-4y+15=0.
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
已知复数z满足(1+i)z=i,则z=( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知数列{an}中,a2=7,且an=an+1-6(n∈N*),则前n项和Sn=( )
A、
| ||
| B、n2 | ||
C、
| ||
| D、3n2-2n |
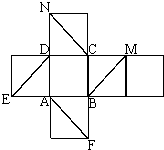 如图是正方体的平面展开图,在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是
如图是正方体的平面展开图,在这个正方体中,①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.以上四个命题中,正确命题的序号是