题目内容
8.△ABC内接于以O为圆心,1为半径的圆,且3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow{0}$.(1)求$\overrightarrow{OB}$•$\overrightarrow{OC}$;$\overrightarrow{OC}$•$\overrightarrow{OA}$
(2)求△AOB的面积.
分析 (1)由3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow{0}$得-3$\overrightarrow{OA}$=4$\overrightarrow{OB}$+5$\overrightarrow{OC}$,两边平方即可得出$\overrightarrow{OB}•\overrightarrow{OC}$,同理可求出$\overrightarrow{OA}•\overrightarrow{OC}$;
(2)利用(1)中的方法求出$\overrightarrow{OA}•\overrightarrow{OB}$,得出$\overrightarrow{OA},\overrightarrow{OB}$的夹角,代入面积公式进行计算.
解答 解:(1)|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=|$\overrightarrow{OC}$|=1,∵3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow{0}$,∴-3$\overrightarrow{OA}$=4$\overrightarrow{OB}$+5$\overrightarrow{OC}$,∴(-3$\overrightarrow{OA}$)2=(4$\overrightarrow{OB}$+5$\overrightarrow{OC}$)2,即9=16+40$\overrightarrow{OB}•\overrightarrow{OC}$+25,∴$\overrightarrow{OB}•\overrightarrow{OC}$=-$\frac{4}{5}$.
∵3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow{0}$,∴-4$\overrightarrow{OB}$=3$\overrightarrow{OA}$+5$\overrightarrow{OC}$,∴(-4$\overrightarrow{OB}$)2=(3$\overrightarrow{OA}$+5$\overrightarrow{OC}$)2,即16=9+30$\overrightarrow{OA}•\overrightarrow{OC}$+25,∴$\overrightarrow{OA}•\overrightarrow{OC}$=-$\frac{3}{5}$.
(2)∵3$\overrightarrow{OA}$+4$\overrightarrow{OB}$+5$\overrightarrow{OC}$=$\overrightarrow{0}$,∴-5$\overrightarrow{OC}$=3$\overrightarrow{OA}$+4$\overrightarrow{OB}$,∴25=9+24$\overrightarrow{OA}•\overrightarrow{OB}$+16,∴$\overrightarrow{OA}•\overrightarrow{OB}$=0.∴OA⊥OB.
∴S△AOB=$\frac{1}{2}$•OA•OB=$\frac{1}{2}$.
点评 本题考查了平面向量的数量积运算,合理利用OA=OB=OC=1是关键,属于基础题.

| A. | 23 | B. | 95 | C. | 135 | D. | 138 |
| A. | (-$\frac{1}{2}$)2015 | B. | ($\frac{1}{2}$)2015 | C. | ($\frac{1}{2}$)2014 | D. | (-$\frac{1}{2}$)2014 |
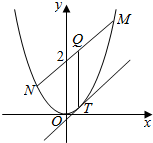 已知抛物线C:x${\;}^{2}=\frac{1}{2}y$,直线y=kx+2交C于M、N两点,Q是线段MN的中点,过Q作x轴的垂线交C于点T.
已知抛物线C:x${\;}^{2}=\frac{1}{2}y$,直线y=kx+2交C于M、N两点,Q是线段MN的中点,过Q作x轴的垂线交C于点T.