题目内容
2.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,右顶点A(2,0).(1)求椭圆C的方程;
(2)过点$M(\frac{3}{2},0)$的直线l交椭圆于B、D两点,设直线AB斜率为k1,直线AD斜率为k2.求证:k1k2为定值,并求此定值.
分析 (Ⅰ)由椭圆离心率为$\frac{{\sqrt{3}}}{2}$,右顶点A(2,0),列出方程组求出a,b,由此能求出椭圆C的方程.
(Ⅱ)由题意知直线l斜率不为0,可设直线l方程为$x=my+\frac{3}{2}$,与椭圆联立,得$({m^2}+4){y^2}+3my-\frac{7}{4}=0$,由此利用根的判别式、韦达定理,结合已知条件能证明k1k2为定值,并能求出此定值.
解答 解:(Ⅰ)∵椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,右顶点A(2,0),
∴由题意得$\left\{\begin{array}{l}{a^2}={b^2}+{c^2}\\ \frac{c}{a}=\frac{{\sqrt{3}}}{2}\\ a=2\end{array}\right.$,解得$\left\{\begin{array}{l}a=2.\\ b=1\\ c=\sqrt{3}.\end{array}\right.$
∴椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$.…(4分)
证明:(Ⅱ)由题意知直线l斜率不为0,可设直线l方程为$x=my+\frac{3}{2}$,
与$\frac{x^2}{4}+{y^2}=1$联立,得$({m^2}+4){y^2}+3my-\frac{7}{4}=0$,
△=9m2+7(m2+4)>0,设B(x1,y1),D(x2,y2),
则${y_1}+{y_2}=\frac{-3m}{{{m^2}+4}},{y_1}{y_2}=\frac{{-\frac{7}{4}}}{{{m^2}+4}}$…(8分)
${k_1}{k_2}=\frac{{{y_1}{y_2}}}{{({x_1}-2)({x_2}-2)}}=\frac{{{y_1}{y_2}}}{{(m{y_1}-\frac{1}{2})(m{y_2}-\frac{1}{2})}}=\frac{{{y_1}{y_2}}}{{{m^2}{y_1}{y_2}-\frac{1}{2}m({y_1}+{y_2})+\frac{1}{4}}}$
=$\frac{{-\frac{7}{4}}}{{-\frac{7}{4}{m^2}+\frac{3}{2}{m^2}+\frac{1}{4}({m^2}+4)}}=-\frac{7}{4}$.
∴k1k2为定值,定值为$-\frac{7}{4}$…(12分)
点评 本题考查椭圆方程的求法,是中档题,解题时要认真审题,注意椭圆性质、根的判别式、韦达定理的合理运用.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
(Ⅰ)求角B的值;
(Ⅱ)若b=2,求a2+c2的最大值,并求取得最大值时角A,C的值.
| A. | 2 | B. | 4 | C. | 2015 | D. | 2016 |
| A. | 45 | B. | 171 | C. | 182 | D. | 192 |
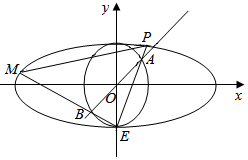 如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π.椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A,B,直线EA,EB与椭圆C1的另一个交点分别是点P,M.
如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π.椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A,B,直线EA,EB与椭圆C1的另一个交点分别是点P,M.