题目内容

14．等差数列{an}的前n项和为Sn，若$\frac{{S}_{2016}}{2016}$=$\frac{{S}_{2015}}{2015}$+2，则数列{an}的公差为（　　）
A．2B．4C．2015D．2016

分析 由题意可得公差d的方程，解方程可得．

解答 解：设数列{an}的公差为d，则由$\frac{{S}_{2016}}{2016}$=$\frac{{S}_{2015}}{2015}$+2可得：
$\frac{2016{a}_{1}+\frac{2016×2015}{2}d}{2016}$=$\frac{2015{a}_{1}+\frac{2015×2014}{2}d}{2015}$+2，
化简可得a1+$\frac{2015}{2}$d=a1+1007d+2，解得d=4，
故选：B．

点评 本题考查等差数列的通项公式和求和公式，属基础题．

练习册系列答案
相关题目
4．己知两点A（2，0），B（-2，0），直线l过点B且与x轴垂直，点C是l上异于点B的动点，直线BP垂直线段OC并交线段AC于点P，记点P的轨迹为曲线Γ．
（1）求曲线Γ的方程；
（2）过点D（-1，0）的直线与曲线 Γ交于M，N两点，直线AM，AN分别与l交于E，F两点．当△AEF的面积是△AMN的面积的2倍时，求直线MN的方程．
5．已知全集U=R，集合A={0，1，2，3，4}，B={x|0＜x＜3}，则如图中阴影部分所表示的集合为（　　）
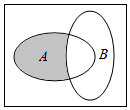
A．{0，1，2}B．{0，1，}C．{0，3，4}D．{3，4}
2．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{{\sqrt{3}}}{2}$，右顶点A（2，0）．
（1）求椭圆C的方程；
（2）过点$M（\frac{3}{2}，0）$的直线l交椭圆于B、D两点，设直线AB斜率为k1，直线AD斜率为k2．求证：k1k2为定值，并求此定值．
9．已知某几何体的三视图如图所示，则该几何体的体积为（　　）
A．$\frac{8π}{3}$B．3πC．$\frac{10π}{3}$D．$\frac{11π}{3}$
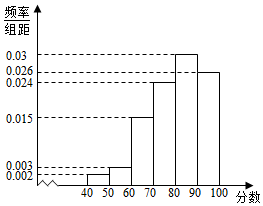19．作为市政府为民办实事之一的公共自行车建设工作已经基本完成了，相关部门准备对该项目进行验收，验收的硬性指标是：市民对该项目的满意指数不低于0.8，否则该项目需进行整改，该部门为了了解市民对该项目的满意程度，在公共自行车自助点随机访问了前来使用的100名市民，并根据这100名市民对该项目满意程度的评分（满分100分），绘制了如图频率分布直方图：
（1）为了了解部分市民对公共自行车建设项目评分较低的原因，该部门从评分低于60分的市民中随机抽取2人进行座谈，求这2人评分恰好都在[50，60）的概率；
（2）根据你所学的统计知识，判断该项目能否通过验收，并说明理由．
（注：满意指数=$\frac{满意程度的平均得分}{100}$）
6．下列函数为偶函数的是（　　）
A．f（x）=x2-xB．f（x）=xcosxC．f（x）=xsinxD．$f（x）=1g（{x+\sqrt{{x^2}+1}}）$
3．圆台的侧面积为$\frac{16}{3}$πcm2，它的内切球的表面积是4πcm2，则圆台的体积为$\frac{26}{9}$πcm3．
4．等差数列-6，-1，4，9，…中的第20项为（　　）
A．89B．-101C．101D．-89

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网