题目内容

11．以正方体的顶点及各面的中心为顶点的三棱锥的个数为956．

分析 首先从8个顶点和4个面为中心的点中选4个，共有C 14 4 种结果，在这些结果中，去掉四点共面的情况，能求出结果．

解答 解：首先从8个顶点和6个面为中心的点中选4个，共有C14 4 种结果，
在这些结果中，有四点共面的情况：
①每个表面有5个点，从中任取4点有${C}_{5}^{4}$=5，即每个表面有5个四点共面，
从而6个表面有6×5=30个四点共面；
②每个对角面有一个四点共面，故6个对角面有6个四点共面；
③全是面的中心的4点共面有3个；
④一条棱上的两点与两个中心共面的情况有6个，且这6个都是对角面，
∴满足条件的结果有C14 4-30-6-3-6=956．
故答案为：956．

点评 本题考查满足条件的三棱锥的个数的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案
相关题目
1．已知正项数列{an}的前n项和Sn满足6Sn=an2+3an+2，且a2是a1和a6的等比中项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）符合[x]表示不超过实数x的最大整数，如[log23]=1，[log25]=2．记${b_n}=[{log_2}\frac{{{a_n}+5}}{3}]$，求数列$\{{2^n}•{b_{2^n}}\}$的前n项和Tn．
2．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{{\sqrt{3}}}{2}$，右顶点A（2，0）．
（1）求椭圆C的方程；
（2）过点$M（\frac{3}{2}，0）$的直线l交椭圆于B、D两点，设直线AB斜率为k1，直线AD斜率为k2．求证：k1k2为定值，并求此定值．
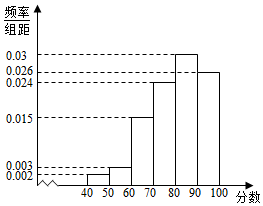19．作为市政府为民办实事之一的公共自行车建设工作已经基本完成了，相关部门准备对该项目进行验收，验收的硬性指标是：市民对该项目的满意指数不低于0.8，否则该项目需进行整改，该部门为了了解市民对该项目的满意程度，在公共自行车自助点随机访问了前来使用的100名市民，并根据这100名市民对该项目满意程度的评分（满分100分），绘制了如图频率分布直方图：
（1）为了了解部分市民对公共自行车建设项目评分较低的原因，该部门从评分低于60分的市民中随机抽取2人进行座谈，求这2人评分恰好都在[50，60）的概率；
（2）根据你所学的统计知识，判断该项目能否通过验收，并说明理由．
（注：满意指数=$\frac{满意程度的平均得分}{100}$）
6．下列函数为偶函数的是（　　）
A．f（x）=x2-xB．f（x）=xcosxC．f（x）=xsinxD．$f（x）=1g（{x+\sqrt{{x^2}+1}}）$
16．已知圆C：（x-1）2+（y-2）2=25，直线l：（2m+1）x+（m+1）y-7m-4=0（m∈R）．
（1）求证：直线l恒过定点；
（2）判断直线l与圆C的位置关系；
（3）当m=0时，求直线l被圆C截得的弦长．
3．圆台的侧面积为$\frac{16}{3}$πcm2，它的内切球的表面积是4πcm2，则圆台的体积为$\frac{26}{9}$πcm3．
20．函数y=sin（$\frac{π}{3}$-2x）+sin2x的最小正周期是（　　）
A．$\frac{π}{2}$B．πC．2πD．4π
1．下列函数为奇函数的是（　　）
A．y=2x-$\frac{1}{{2}^{x}}$B．y=ln$\sqrt{1-{x}^{2}}$C．y=x2-2xD．y=x2+2x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网